Ő‚ńŅńŕ»›
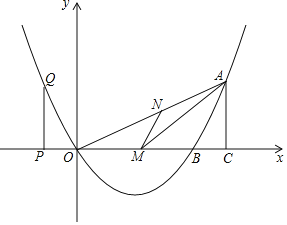
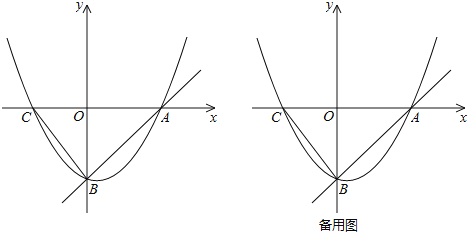
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪŌŖy£Ĺx©Ā4”Žx÷Š°Ęy÷Š∑÷ĪūĹĽ”ŕA°ĘBŃĹĶ„£¨Ň◊őÔŌŖy£Ĺ![]() x2+bx+cĺ≠ĻżA°ĘBŃĹĶ„£¨”Žx÷ŠĶńŃŪ“ĽłŲĹĽĶ„ő™C£¨Ń¨Ĺ”BC£ģ
x2+bx+cĺ≠ĻżA°ĘBŃĹĶ„£¨”Žx÷ŠĶńŃŪ“ĽłŲĹĽĶ„ő™C£¨Ń¨Ĺ”BC£ģ
£®1£©«ůŇ◊őÔŌŖĶńĹ‚őŲ ĹľįĶ„CĶń◊ÝĪÍ£Ľ
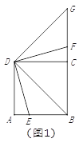
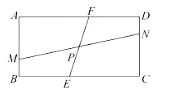
£®2£©Ķ„M‘ŕŇ◊őÔŌŖ…Ō£¨Ń¨Ĺ”MB£¨ĶĪ°ŌMBA+°ŌCBO£Ĺ45°„ Ī£¨«ůĶ„MĶń◊ÝĪÍ£Ľ
£®3£©Ķ„Pī”Ķ„C≥Ų∑Ę£¨—ōŌŖ∂őCA”…CŌÚA‘ň∂Į£¨Õ¨ ĪĶ„Qī”Ķ„B≥Ų∑Ę£¨—ōŌŖ∂őBC”…BŌÚC‘ň∂Į£¨P°ĘQĶń‘ň∂ĮňŔ∂»∂ľ «√Ņ√Ž1łŲĶ•őĽ≥§∂»£¨ĶĪQĶ„ĶĹīÔCĶ„ Ī£¨P°ĘQÕ¨ ĪÕ£÷Ļ‘ň∂Į£¨ ‘ő ‘ŕ◊ÝĪÍ∆Ĺ√śńŕ «∑Ůīś‘ŕĶ„D£¨ ĻP°ĘQ‘ň∂ĮĻż≥Ő÷–Ķńń≥“Ľ ĪŅŐ£¨“‘C°ĘD°ĘP°ĘQő™∂•Ķ„ĶńňńĪŖ–őő™Ń‚–ő£Ņ»Űīś‘ŕ£¨÷ĪĹ”–ī≥ŲĶ„DĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©y£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā4£¨C£®©Ā3£¨0£©£Ľ£®2£©¬ķ◊„ŐűľĢĶńĶ„MĶń◊ÝĪÍő™£®
x©Ā4£¨C£®©Ā3£¨0£©£Ľ£®2£©¬ķ◊„ŐűľĢĶńĶ„MĶń◊ÝĪÍő™£®![]() £¨©Ā
£¨©Ā![]() £©ĽÚ£®5£¨
£©ĽÚ£®5£¨![]() £©£Ľ£®3£©īś‘ŕ¬ķ◊„ŐűľĢĶńĶ„D£¨Ķ„D◊ÝĪÍő™£®©Ā
£©£Ľ£®3£©īś‘ŕ¬ķ◊„ŐűľĢĶńĶ„D£¨Ķ„D◊ÝĪÍő™£®©Ā![]() £¨©Ā
£¨©Ā![]() £©ĽÚ£®1£¨©Ā2£©ĽÚ£®©Ā
£©ĽÚ£®1£¨©Ā2£©ĽÚ£®©Ā![]() £¨
£¨![]() £©£ģ
£©£ģ
°ĺĹ‚őŲ°Ņ
Ķŕ“Ľő «ůĹ‚őŲ Ĺ÷ų“™ņŻ”√īż∂®ŌĶ ż«ůĹ‚£¨ņŻ”√“ĽīőļĮ ży£Ĺx©Ā4£¨«ůĹ‚≥ŲAĶ„◊ÝĪÍļÕBĶ„◊ÝĪÍ£¨»Ľļůīķ»Ž∑Ĺ≥ŐľīŅ…£¨
Ķŕ∂Ģő «ůĹ‚MĶ„Ķń◊ÝĪÍ£¨–Ť“™Ő÷¬Ř£¨“Úő™°ŌMBA+°ŌCBO£Ĺ45°„ «∂ĮŐ¨Ķń£¨Ļ ĶĪBM°ÕBC Ī «“Ľ÷÷«ťŅŲ£¨ņŻ”√tan°ŌM1BE£Ĺtan°ŌBCO£Ĺ![]() £¨Ņ…“‘łÝ≥ŲĶ» ĹĻōŌĶ£¨«ů≥ŲMĶ„£¨BM”ŽBCĻō”ŕy÷Š∂‘≥∆ Ī «Ķŕ∂Ģ÷÷«ťŅŲ£¨tan°ŌM2BE£Ĺtan°ŌCBO£Ĺ
£¨Ņ…“‘łÝ≥ŲĶ» ĹĻōŌĶ£¨«ů≥ŲMĶ„£¨BM”ŽBCĻō”ŕy÷Š∂‘≥∆ Ī «Ķŕ∂Ģ÷÷«ťŅŲ£¨tan°ŌM2BE£Ĺtan°ŌCBO£Ĺ![]() £¨Ņ…“‘≥ŲłÝĶ» ĹĻōŌĶ£¨«ů≥ŲMĶ„
£¨Ņ…“‘≥ŲłÝĶ» ĹĻōŌĶ£¨«ů≥ŲMĶ„
Ķ໿ő £¨–Ť“™Ő÷¬Ř£¨“Úő™ňńłŲĶ„£¨÷™ŌĢ∆š÷–»żłŲĶ„£¨Ņ…“‘’‚—ýŐ÷¬Ř£¨ĶĪCPő™Ń‚–őĶńĪŖ£¨CQő™∂‘Ĺ«ŌŖ’‚ «Ķŕ“Ľ÷÷«ťŅŲ£¨ņŻ”√Ĺ‚÷ĪĹ«»żĹ«–ő«ů≥ŲQĶ„Ķń◊›◊ÝĪÍ£¨ĺÕ÷™ĶņDĶ„Ķń◊›◊ÝĪÍ£¨»ĽļůņŻ”√cos°ŌBCO£Ĺ![]() £¨Ĺ®ŃĘĶ» ĹľīŅ…«ů≥ŲŃ‚–őĶńĪŖ≥§£¨ņŻ”√Ń‚–őĪŖ≥§ļÕQĶ„ļŠ◊ÝĪÍ£¨ľīŅ…Ķ√ĶĹQĶ„ļŠ◊ÝĪÍ£¨ĶĪCQļÕCPĺýő™Ń‚–őĶńĪŖ’‚ «Ķŕ∂Ģ÷÷«ťŅŲ£¨“Úő™CP=CQ=BQ£¨ňý“‘QĶ„‘ŕBCĶń÷–£¨ľīŃ‚–őĶńĪŖ≥§≥ŲņīŃň£¨ņŻ”√Ĺ‚÷ĪĹ«»żĹ«–őľīŅ…łÝ≥ŲQĶ„Ķń◊›◊ÝĪÍ£¨÷™ĶņŃ‚–őĶńĪŖ≥§£¨ňý“‘DĶ„ĶńļŠ◊›◊ÝĪÍ∂ľ≥ŲņīŃň£¨ĶĪCQő™Ń‚–őĶńĪŖ£¨CPő™Ń‚–őĶń∂‘Ĺ«ŌŖ’‚ «Ķ໿÷÷«ťŅŲ£¨ņŻ”√Ĺ‚÷ĪĹ«»żĹ«–ő£¨Ņ…“‘łÝ≥ŲQĶ„◊ÝĪÍ£¨ő“√«Ņ…“‘÷™ĶņDĶ„ļÕQĶ„Ļō”ŕx÷Š∂‘≥∆£¨”–Ń‚–őĶńĽýĪĺ–‘÷ Ņ…“‘÷™Ķņ£¨ňý“‘DĶ„◊ÝĪÍ≥ŲņīŃň
£¨Ĺ®ŃĘĶ» ĹľīŅ…«ů≥ŲŃ‚–őĶńĪŖ≥§£¨ņŻ”√Ń‚–őĪŖ≥§ļÕQĶ„ļŠ◊ÝĪÍ£¨ľīŅ…Ķ√ĶĹQĶ„ļŠ◊ÝĪÍ£¨ĶĪCQļÕCPĺýő™Ń‚–őĶńĪŖ’‚ «Ķŕ∂Ģ÷÷«ťŅŲ£¨“Úő™CP=CQ=BQ£¨ňý“‘QĶ„‘ŕBCĶń÷–£¨ľīŃ‚–őĶńĪŖ≥§≥ŲņīŃň£¨ņŻ”√Ĺ‚÷ĪĹ«»żĹ«–őľīŅ…łÝ≥ŲQĶ„Ķń◊›◊ÝĪÍ£¨÷™ĶņŃ‚–őĶńĪŖ≥§£¨ňý“‘DĶ„ĶńļŠ◊›◊ÝĪÍ∂ľ≥ŲņīŃň£¨ĶĪCQő™Ń‚–őĶńĪŖ£¨CPő™Ń‚–őĶń∂‘Ĺ«ŌŖ’‚ «Ķ໿÷÷«ťŅŲ£¨ņŻ”√Ĺ‚÷ĪĹ«»żĹ«–ő£¨Ņ…“‘łÝ≥ŲQĶ„◊ÝĪÍ£¨ő“√«Ņ…“‘÷™ĶņDĶ„ļÕQĶ„Ļō”ŕx÷Š∂‘≥∆£¨”–Ń‚–őĶńĽýĪĺ–‘÷ Ņ…“‘÷™Ķņ£¨ňý“‘DĶ„◊ÝĪÍ≥ŲņīŃň
£®1£©÷ĪŌŖĹ‚őŲ Ĺy£Ĺx©Ā4£¨
ŃÓx£Ĺ0£¨Ķ√y£Ĺ©Ā4£Ľ
ŃÓy£Ĺ0£¨Ķ√x£Ĺ4£ģ
°ŗA£®4£¨0£©°ĘB£®0£¨©Ā4£©£ģ
°ŖĶ„A°ĘB‘ŕŇ◊őÔŌŖy£Ĺ![]() x2+bx+c…Ō£¨
x2+bx+c…Ō£¨
°ŗ
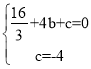 £¨
£¨
Ĺ‚Ķ√![]() £¨
£¨
°ŗŇ◊őÔŌŖĹ‚őŲ Ĺő™£ļy£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā4£ģ
x©Ā4£ģ
ŃÓy£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā4£Ĺ0£¨
x©Ā4£Ĺ0£¨
Ĺ‚Ķ√£ļx£Ĺ©Ā3ĽÚx£Ĺ4£¨
°ŗC£®©Ā3£¨0£©£ģ
£®2£©°ŌMBA+°ŌCBO£Ĺ45°„£¨
…ŤM£®x£¨y£©£¨
ĘŔĶĪBM°ÕBC Ī£¨»ÁīūÕľ2©Ā1ňý ĺ£ģ
°Ŗ°ŌABO£Ĺ45°„£¨
°ŗ°ŌMBA+°ŌCBO£Ĺ45°„£¨Ļ Ķ„M¬ķ◊„ŐűľĢ£ģ
ĻżĶ„M1◊ųM1E°Õy÷Š”ŕĶ„E£¨‘ÚM1E£Ĺx£¨OE£Ĺ©Āy£¨
°ŗBE£Ĺ4+y£ģ
°Ŗtan°ŌM1BE£Ĺtan°ŌBCO£Ĺ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ÷ĪŌŖBM1ĶńĹ‚őŲ Ĺő™£ļy£Ĺ![]() x©Ā4£ģ
x©Ā4£ģ
Ń™ŃĘy£Ĺ![]() x©Ā4”Žy£Ĺ
x©Ā4”Žy£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā4£¨
x©Ā4£¨
Ķ√£ļ![]() x©Ā4£Ĺ
x©Ā4£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā4£¨
x©Ā4£¨
Ĺ‚Ķ√£ļx1£Ĺ0£¨x2£Ĺ![]() £¨
£¨
°ŗy1£Ĺ©Ā4£¨y2£Ĺ©Ā![]() £¨
£¨
°ŗM1£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ
£©£Ľ
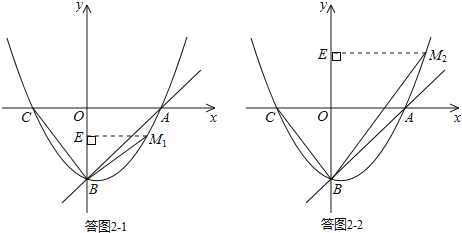
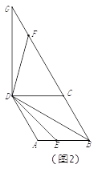
ĘŕĶĪBM”ŽBCĻō”ŕy÷Š∂‘≥∆ Ī£¨»ÁīūÕľ2©Ā2ňý ĺ£ģ
°Ŗ°ŌABO£Ĺ°ŌMBA+°ŌMBO£Ĺ45°„£¨°ŌMBO£Ĺ°ŌCBO£¨
°ŗ°ŌMBA+°ŌCBO£Ĺ45°„£¨
Ļ Ķ„M¬ķ◊„ŐűľĢ£ģ
ĻżĶ„M2◊ųM2E°Õy÷Š”ŕĶ„E£¨
‘ÚM2E£Ĺx£¨OE£Ĺy£¨
°ŗBE£Ĺ4+y£ģ
°Ŗtan°ŌM2BE£Ĺtan°ŌCBO£Ĺ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗ÷ĪŌŖBM2ĶńĹ‚őŲ Ĺő™£ļy£Ĺ![]() x©Ā4£ģ
x©Ā4£ģ
Ń™ŃĘy£Ĺ![]() x©Ā4”Žy£Ĺ
x©Ā4”Žy£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā4Ķ√£ļ
x©Ā4Ķ√£ļ![]() x©Ā4£Ĺ
x©Ā4£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā4£¨
x©Ā4£¨
Ĺ‚Ķ√£ļx1£Ĺ0£¨x2£Ĺ5£¨
°ŗy1£Ĺ©Ā4£¨y2£Ĺ![]() £¨
£¨
°ŗM2£®5£¨![]() £©£ģ
£©£ģ
◊Ř…Ōňý Ų£¨¬ķ◊„ŐűľĢĶńĶ„MĶń◊ÝĪÍő™£ļ£®![]() £¨©Ā
£¨©Ā![]() £©ĽÚ£®5£¨
£©ĽÚ£®5£¨![]() £©£ģ
£©£ģ
£®3£©…Ť°ŌBCO£Ĺ¶»£¨‘Útan¶»£Ĺ![]() £¨sin¶»£Ĺ
£¨sin¶»£Ĺ![]() £¨cos¶»£Ĺ
£¨cos¶»£Ĺ![]() £ģ
£ģ
ľŔ…Ťīś‘ŕ¬ķ◊„ŐűľĢĶńĶ„D£¨…ŤŃ‚–őĶń∂‘Ĺ«ŌŖĹĽ”ŕĶ„E£¨…Ť‘ň∂Į Īľšő™t£ģ
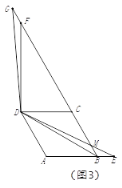
ĘŔ»Ű“‘CQő™Ń‚–ő∂‘Ĺ«ŌŖ£¨»ÁīūÕľ3©Ā1£ģīň ĪBQ£Ĺt£¨Ń‚–őĪŖ≥§£Ĺt£ģ
°ŗCE£Ĺ![]() CQ£Ĺ
CQ£Ĺ![]() £®5©Āt£©£ģ
£®5©Āt£©£ģ
‘ŕRt°ųPCE÷–£¨cos¶»£Ĺ![]() £Ĺ
£Ĺ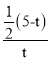 £Ĺ
£Ĺ![]() £¨
£¨
Ĺ‚Ķ√t£Ĺ![]() £ģ
£ģ
°ŗCQ£Ĺ5©Āt£Ĺ![]() £ģ
£ģ
ĻżĶ„Q◊ųQF°Õx÷Š”ŕĶ„F£¨
‘ÚQF£ĹCQsin¶»£Ĺ![]() £¨CF£ĹCQcos¶»£Ĺ
£¨CF£ĹCQcos¶»£Ĺ![]() £¨
£¨
°ŗOF£Ĺ3©ĀCF£Ĺ![]() £ģ
£ģ
°ŗQ£®©Ā![]() £¨©Ā
£¨©Ā![]() £©£ģ
£©£ģ
°ŖĶ„D1”ŽĶ„QļŠ◊ÝĪÍŌŗ≤ÓtłŲĶ•őĽ£¨
°ŗD1£®©Ā![]() £¨©Ā
£¨©Ā![]() £©£Ľ
£©£Ľ
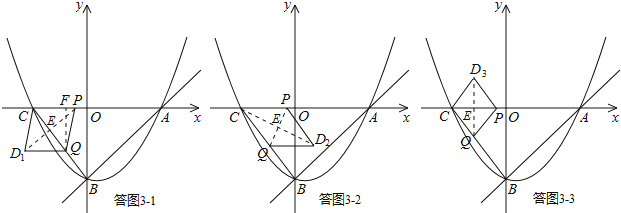
Ęŕ»Ű“‘PQő™Ń‚–ő∂‘Ĺ«ŌŖ£¨»ÁīūÕľ3©Ā2£ģīň ĪBQ£Ĺt£¨Ń‚–őĪŖ≥§£Ĺt£ģ
°ŖBQ£ĹCQ£Ĺt£¨
°ŗt£Ĺ![]() £¨Ķ„Qő™BC÷–Ķ„£¨
£¨Ķ„Qő™BC÷–Ķ„£¨
°ŗQ£®©Ā![]() £¨©Ā2£©£ģ
£¨©Ā2£©£ģ
°ŖĶ„D2”ŽĶ„QļŠ◊ÝĪÍŌŗ≤ÓtłŲĶ•őĽ£¨
°ŗD2£®1£¨©Ā2£©£Ľ
Ęػۓ‘CPő™Ń‚–ő∂‘Ĺ«ŌŖ£¨»ÁīūÕľ3©Ā3£ģīň ĪBQ£Ĺt£¨Ń‚–őĪŖ≥§£Ĺ5©Āt£ģ
‘ŕRt°ųCEQ÷–£¨cos¶»£Ĺ![]() £Ĺ
£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
Ĺ‚Ķ√t£Ĺ![]() £ģ
£ģ
°ŗOE£Ĺ3©ĀCE£Ĺ3©Ā![]() t£Ĺ
t£Ĺ![]() £¨D3E£ĹQE£ĹCQsin¶»£Ĺ£®5©Ā
£¨D3E£ĹQE£ĹCQsin¶»£Ĺ£®5©Ā![]() £©°Ń
£©°Ń![]() £Ĺ
£Ĺ![]() £ģ
£ģ
°ŗD3£®©Ā![]() £¨
£¨![]() £©£ģ
£©£ģ
◊Ř…Ōňý Ų£¨īś‘ŕ¬ķ◊„ŐűľĢĶńĶ„D£¨Ķ„D◊ÝĪÍő™£ļ£®©Ā![]() £¨©Ā
£¨©Ā![]() £©ĽÚ£®1£¨©Ā2£©ĽÚ£®©Ā
£©ĽÚ£®1£¨©Ā2£©ĽÚ£®©Ā![]() £¨
£¨![]() £©£ģ
£©£ģ

 Ľ•∂Į”Ę”ÔŌĶŃ–īūįł
Ľ•∂Į”Ę”ÔŌĶŃ–īūįł