题目内容
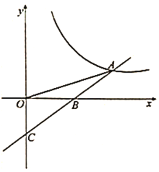
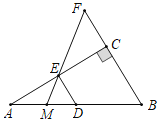
【题目】⑴如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转90°,旋转后角的两边分别与射线
逆时针旋转90°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①线段![]() 和
和![]() 的数量关系是 ;
的数量关系是 ;
②写出线段![]() 和
和![]() 之间的数量关系.
之间的数量关系.
⑵当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转120°,旋转后角的两边分别与射线
逆时针旋转120°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
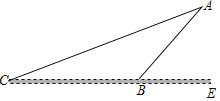
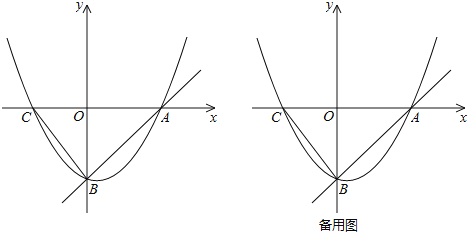
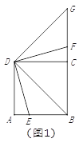
①如图2,点![]() 在线段上时,请探究线段
在线段上时,请探究线段![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
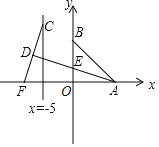
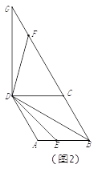
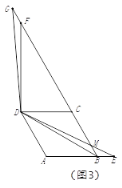
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ;若
;若 ![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
【答案】⑴①![]() ; ②
; ②![]() ;⑵①
;⑵①![]() . 理由见解析,②
. 理由见解析,②![]() 的长度为
的长度为![]() . 理由见解析.
. 理由见解析.
【解析】
(1)①根据旋转的性质解答即可;
②根据正方形的性质和全等三角形的判定和性质解答即可;
(2)①根据菱形的性质和全等三角形的判定和性质解答即可;
②作辅助线,计算BD和BF的长,根据平行线分线段成比例定理可得BM的长,根据线段的差可得结论.
(1)①DB=DG,理由是:
∵∠DBE绕点B逆时针旋转90°,如图1,
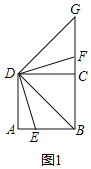
由旋转可知,∠BDE=∠FDG,∠BDG=90°,
∵四边形ABCD是正方形,
∴∠CBD=45°,
∴∠G=45°,
∴∠G=∠CBD=45°,
∴DB=DG;
故答案为:DB=DG;
②BF+BE=![]() BD,理由如下:
BD,理由如下:
由①知:∠FDG=∠EDB,∠G=∠DBE=45°,BD=DG,
∴△FDG≌△EDB(ASA),
∴BE=FG,
∴BF+FG=BF+BE=BC+CG,
Rt△DCG中,∵∠G=∠CDG=45°,
∴CD=CG=CB,
∵DG=BD=![]() BC,
BC,
即BF+BE=2BC=![]() BD;
BD;
(2)①如图2,BF+BE=![]() BD,
BD,
理由如下:在菱形ABCD中,∠ADB=∠CDB=![]() ∠ADC=
∠ADC=![]() ×60°=30°,
×60°=30°,
由旋转120°得∠EDF=∠BDG=120°,∠EDB=∠FDG,
在△DBG中,∠G=180°-120°-30°=30°,
∴∠DBG=∠G=30°,
∴DB=DG,
∴△EDB≌△FDG(ASA),
∴BE=FG,
∴BF+BE=BF+FG=BG,
过点D作DM⊥BG于点M,如图2,
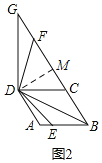
∵BD=DG,
∴BG=2BM,
在Rt△BMD中,∠DBM=30°,
∴BD=2DM.
设DM=a,则BD=2a,
DM=![]() a,
a,
∴BG=2![]() a,
a,
∴![]() ,
,
∴BG=![]() BD,
BD,
∴BF+BE=BG=![]() BD;
BD;
②过点A作AN⊥BD于N,过D作DP⊥BG于P,如图3,
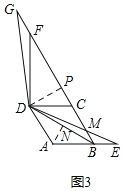
Rt△ABN中,∠ABN=30°,AB=2,
∴AN=1,BN=![]() ,
,
∴BD=2BN=2![]() ,
,
∵DC∥BE,
∴![]() ,
,
∵CM+BM=2,
∴BM=![]() ,
,
Rt△BDP中,∠DBP=30°,BD=2![]() ,
,
∴BP=3,
由旋转得:BD=BF,
∴BF=2BP=6,
∴GM=BG-BM=6+1-![]() =
=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某食品公司为迎接端午节,特别推出了几种新的粽子,并在一超市开展“品尝”活动,要求参加“品尝”活动的每一位顾客都选择一种新粽子而且只能选择一种新粽子,为了解市民对新粽子的喜欢程度,该食品公司随机抽取了参加“品尝”活动的部分顾客,进行“我最喜欢的新粽子”问卷调查,并将调查结果绘制成如下两个完整的统计图表.
参加“品尝”活动部分顾客“我最喜欢的粽子”调查结果统计表
新粽子名称 | “品尝”人数 |
香芋粽 |
|
水果粽 |
|
莲子粽 |
|
香菇粽 |
|
鲍鱼粽 |
|
火腿粽 |
|
排骨粽 |
|
参加“品尝”活动部分顾客“我最喜欢的粽子”调查结果统计表
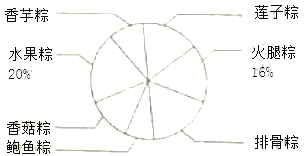
请解答下列问题:
(1)![]() _______,
_______,![]() _______.
_______.
(2)在扇形统计图中,“香芋粽”所对应的扇形圆心角为_______度.
(3)若参加“品尝”活动的顾客共有![]() 人,“品尝”某种新粽子的人数不低于
人,“品尝”某种新粽子的人数不低于![]() 人才可以批量加工,试通过计算估计该食品公司哪种新粽子不能批量加工.
人才可以批量加工,试通过计算估计该食品公司哪种新粽子不能批量加工.