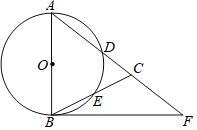
ЬтФПФкШн
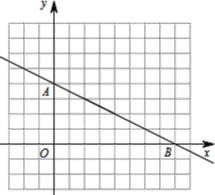
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓЙ§ЕуOЃЈ0ЃЌ0ЃЉЃЎAЃЈ8ЃЌ4ЃЉЃЌгыxжсНЛгкСэвЛЕуBЃЌЧвЖдГЦжсЪЧжБЯпxЃН3ЃЎ
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
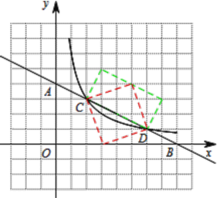
ЃЈ2ЃЉШєMЪЧOBЩЯЕФвЛЕуЃЌзїMNЁЮABНЛOAгкNЃЌЕБЁїANMУцЛ§зюДѓЪБЃЌЧѓMЕФзјБъЃЛ
ЃЈ3ЃЉPЪЧxжсЩЯЕФЕуЃЌЙ§PзїPQЁЭxжсгыХзЮяЯпНЛгкQЃЎЙ§AзїACЁЭxжсгкCЃЌЕБвдOЃЌPЃЌQЮЊЖЅЕуЕФШ§НЧаЮгывдOЃЌAЃЌCЮЊЖЅЕуЕФШ§НЧаЮЯрЫЦЪБЃЌЧѓPЕуЕФзјБъЃЎ
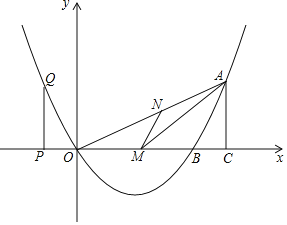
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕБtЃН3ЪБЃЌSЁїAMNгазюДѓжЕ3ЃЌДЫЪБMЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЛђЃЈЉ2ЃЌ0ЃЉЛђЃЈ4ЃЌ0ЃЉЛђЃЈ8ЃЌ0ЃЉЃЎ
ЃЛЃЈ2ЃЉЕБtЃН3ЪБЃЌSЁїAMNгазюДѓжЕ3ЃЌДЫЪБMЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЛђЃЈЉ2ЃЌ0ЃЉЛђЃЈ4ЃЌ0ЃЉЛђЃЈ8ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШРћгУХзЮяЯпЕФЖдГЦадШЗЖЈBЃЈ6ЃЌ0ЃЉЃЌШЛКѓЩшНЛЕуЪНЧѓХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЩшMЃЈtЃЌ0ЃЉЃЌЯШЦфЧѓГіжБЯпOAЕФНтЮіЪНЮЊ![]() жБЯпABЕФНтЮіЪНЮЊy=2x-12ЃЌжБЯпMNЕФНтЮіЪНЮЊy=2x-2tЃЌдйЭЈЙ§НтЗНГЬзщ
жБЯпABЕФНтЮіЪНЮЊy=2x-12ЃЌжБЯпMNЕФНтЮіЪНЮЊy=2x-2tЃЌдйЭЈЙ§НтЗНГЬзщ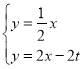 ЕУNЃЈ
ЕУNЃЈ![]() ЃЉЃЌНгзХРћгУШ§НЧаЮУцЛ§ЙЋЪНЃЌРћгУSЁїAMN=SЁїAOM-SЁїNOMЕУЕН
ЃЉЃЌНгзХРћгУШ§НЧаЮУцЛ§ЙЋЪНЃЌРћгУSЁїAMN=SЁїAOM-SЁїNOMЕУЕН![]() ШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
ШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
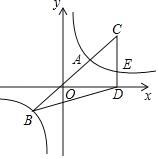
ЃЈ3ЃЉЩшQ![]() ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЃЌЕБ
ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЗНЗЈЃЌЕБ![]() ЪБЃЌЁїPQOЁзЁїCOAЃЌдђ
ЪБЃЌЁїPQOЁзЁїCOAЃЌдђ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌЁїPQOЁзЁїCAOЃЌдђ
ЪБЃЌЁїPQOЁзЁїCAOЃЌдђ![]() ЃЌШЛКѓЗжБ№НтЙигкmЕФОјЖджЕЗНГЬПЩЕУЕНЖдгІЕФPЕузјБъЃЎ
ЃЌШЛКѓЗжБ№НтЙигкmЕФОјЖджЕЗНГЬПЩЕУЕНЖдгІЕФPЕузјБъЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпЙ§дЕуЃЌЖдГЦжсЪЧжБЯпxЃН3ЃЌ
ЁрBЕузјБъЮЊЃЈ6ЃЌ0ЃЉЃЌ
ЩшХзЮяЯпНтЮіЪНЮЊyЃНaxЃЈxЉ6ЃЉЃЌ
АбAЃЈ8ЃЌ4ЃЉДњШыЕУa82ЃН4ЃЌНтЕУaЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊyЃН![]() xЃЈxЉ6ЃЉЃЌМДyЃН
xЃЈxЉ6ЃЉЃЌМДyЃН![]() x2Љ
x2Љ![]() xЃЛ
xЃЛ
ЃЈ2ЃЉЩшMЃЈtЃЌ0ЃЉЃЌ
взЕУжБЯпOAЕФНтЮіЪНЮЊyЃН![]() xЃЌ
xЃЌ
ЩшжБЯпABЕФНтЮіЪНЮЊyЃНkx+bЃЌ
АбBЃЈ6ЃЌ0ЃЉЃЌAЃЈ8ЃЌ4ЃЉДњШыЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊyЃН2xЉ12ЃЌ
ЁпMN/span>ЁЮABЃЌ
ЁрЩшжБЯпMNЕФНтЮіЪНЮЊyЃН2x+nЃЌ
АбMЃЈtЃЌ0ЃЉДњШыЕУ2t+nЃН0ЃЌНтЕУnЃНЉ2tЃЌ
ЁржБЯпMNЕФНтЮіЪНЮЊyЃН2xЉ2tЃЌ
НтЗНГЬзщ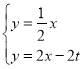 ЕУ
ЕУ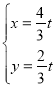 ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЁрSЁїAMNЃНSЁїAOMЉSЁїNOM
![]()
![]()
![]() ЃЌ
ЃЌ
ЕБtЃН3ЪБЃЌSЁїAMNгазюДѓжЕ3ЃЌДЫЪБMЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ
ЁпЁЯOPQЃНЁЯACOЃЌ
ЁрЕБ![]() ЪБЃЌЁїPQOЁзЁїCOAЃЌМД
ЪБЃЌЁїPQOЁзЁїCOAЃЌМД![]() ЃЌ
ЃЌ
ЁрPQЃН2POЃЌМД![]() ЃЌ
ЃЌ
НтЗНГЬ![]() ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН14ЃЌДЫЪБPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЃЛ
ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН14ЃЌДЫЪБPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЃЛ
НтЗНГЬ![]() ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃНЉ2ЃЌДЫЪБPЕузјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЛ
ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃНЉ2ЃЌДЫЪБPЕузјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЛ
ЁрЕБ![]() ЪБЃЌЁїPQOЁзЁїCAOЃЌМД
ЪБЃЌЁїPQOЁзЁїCAOЃЌМД![]() ЃЌ
ЃЌ
ЁрPQЃН![]() POЃЌМД
POЃЌМД![]() ЃЌ
ЃЌ
НтЗНГЬ![]() ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН8ЃЌДЫЪБPЕузјБъЮЊЃЈ8ЃЌ0ЃЉЃЛ
ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН8ЃЌДЫЪБPЕузјБъЮЊЃЈ8ЃЌ0ЃЉЃЛ
НтЗНГЬ![]() ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН4ЃЌДЫЪБPЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЛ
ЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН4ЃЌДЫЪБPЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЛ
злЩЯЫљЪіЃЌPЕузјБъЮЊЃЈ14ЃЌ0ЃЉЛђЃЈЉ2ЃЌ0ЃЉЛђЃЈ4ЃЌ0ЃЉЛђЃЈ8ЃЌ0ЃЉЃЎ

 ГЌФмбЇЕфгІгУЬтЬтПЈЯЕСаД№АИ
ГЌФмбЇЕфгІгУЬтЬтПЈЯЕСаД№АИ