Question

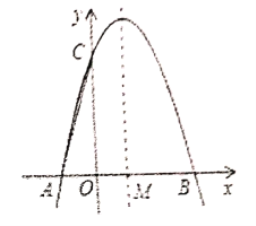
【题目】如图，抛物线与轴交于，两点，与轴交于点，抛物线的对称轴与轴交于点.

（1）求抛物线的函数解析式；

（2）设点是直线上的一个动点，当的值最小时，求的长；

（3）在直线上是否存在点，使以，，为顶点的三角形与相似？若存在，请求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1） （2） （3）存在，点的坐标为或或或，理由见解析

【解析】

（1）由题意先求得C（0，3）．设抛物线的解析式为y=a（x+1）（x-3），将点C的坐标代入可求得a的值即可；

（2）由题意依据轴对称图形的性质可知PA=PB，则PA+PC=PB+PC，则当点P在线段BC上时，PC+AP有最小值，PA+PC的最小值=BC，接下来，依据勾股定理求解即可；

（3）根据题意设点Q的坐标为（1，m），则QM=|m|，然后依据相似三角形的性质可得到∠OQM=∠CAO或∠OQM=∠ACO，然后依据相似三角形的性质列比例求解即可．

解：(1)把代入抛物线中，得

设抛物线的解析式为

将点的坐标代入，得

解得

抛物线的解析式为.

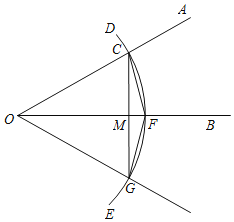
（2）如图所示：

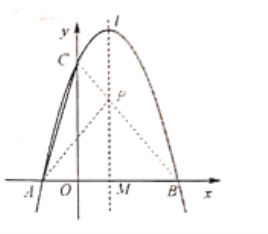
点与点关于直线对称，点在直线上

两点之间线段最短

当点在线段上时，有最小值，

的最小值即为

，

的最小值为.

（3）抛物线的对称轴为直线

设点的坐标为，则

以，，为顶点的三角形与相似，

或

当时，

即，解得

点的坐标为或

当时，

即，解得

点的坐标为或

综上所述，点的坐标为或或或.