��Ŀ����
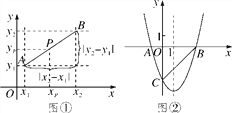
����Ŀ���Ķ����ϣ���ͼ�٣���ƽ��ֱ������ϵ�У�A��B���������ֱ�ΪA(x1��y1)��B(x2��y2)��AB���е�P������Ϊ(xp��yp)����xp��x1��x2��xp����xp��![]() ��ͬ����yp��
��ͬ����yp��![]() ������AB���е�����ΪP(
������AB���е�����ΪP(![]() ,
,![]() ).�ɹ��ɶ�����AB2��|x2��x1|2��|y2��y1|2������A��B�����ľ��빫ʽΪAB��
).�ɹ��ɶ�����AB2��|x2��x1|2��|y2��y1|2������A��B�����ľ��빫ʽΪAB��![]() .
.
ע��������ʽ��A��B��ƽ��ֱ������ϵ������λ��Ҳ������
����������⣺
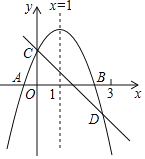
��ͼ�ڣ�������y��ax2��bx��3(a��0)��x�ύ��A��B���㣬��y�ύ�ڵ�C����BO��OC��3AO������BC.
(1)�������ߵı���ʽ��
(2)�������ߵĶԳ������Ƿ���ڵ�P��ʹ��PBC�ǵ��������Σ������ڣ����������������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��x2��2x��3��2��P������Ϊ(1����1)��(1�� ![]() )��(1����
)��(1���� ![]() )��(1����3��
)��(1����3��![]() )��(1����3��
)��(1����3��![]() )
)
�������������������1����������y��ax2��bx��3��y���ڵ�C�������C������Ϊ(0����3)����BO��OC��3AO���ɵõ�B������Ϊ(3��0)����A������Ϊ(��1��0)����Ϊ����������x�ύ��A��B���㣬�������a��b��ֵ��
��2����PBC�ǵ��������Σ�����������������ٵ�PB��PC���ڵ�BC��PB���۵�BC��PCʱ���ۼ���.
���������(1)��������y��ax2��bx��3��y���ڵ�C��
���C������Ϊ(0����3)��
��OC��3.
��BO��OC��3AO��
��BO��3��AO��1��
���B������Ϊ(3��0)����A������Ϊ(��1��0)��
�߸���������x�ύ��A��B���㣬
��![]() ���
���![]() .
.
�������ߵı���ʽΪy��x2��2x��3��
(2)���ڣ���(1)֪������Ϊy��x2��2x��3���Գ���Ϊֱ��x��1.��P�������Ϊ(1��m)��
��B�������Ϊ(3��0)��C�������Ϊ(0����3)��
��BC��3![]() ��PB��
��PB��![]() ��PC��
��PC��![]()
.�ߡ�PBC�ǵ��������Σ����������������
�ٵ�PB��PCʱ����![]() ��
��![]() ��
��
��m����1��
��P�������Ϊ(1����1)��
�ڵ�BC��PBʱ����3![]() ��
��![]() ��
��
��m����![]() ��
��
��P�������Ϊ(1�� ![]() )��(1����
)��(1���� ![]() )��
)��
�۵�BC��PCʱ����3![]() ��
��![]() ��
��
��m����3��![]() ��
��
��P�������Ϊ(1����3��![]() )��(1����3��
)��(1����3��![]() )��
)��
��������������������P������Ϊ(1����1)��(1�� ![]() )��(1����
)��(1���� ![]() )��(1����3��
)��(1����3��![]() )��(1����3��
)��(1����3��![]() )��
)��

����Ŀ����ʮ�Ŵ�������������ҹ����Ӵ�����������Ⱦ�����ȣ�������ɽ��ˮ���������������û����ͽ��������Ϊ���㣬Ϊ�˵���ѧ������������֪ʶ���˽�̶ȣ�ijУ��ȫУѧ���г�ȡ400��ͬѧ����һ�ε��飬���ݵ���ͳ�ƽ���������˲�������һ��ͳ��ͼ����
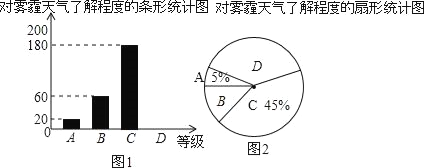
�������˽�̶ȵ�ͳ�Ʊ�
���������˽�̶� | �ٷֱ� |
A���dz��˽� | 5% |
B���Ƚ��˽� | m |
C�������˽� | 45% |
D�����˽� | n |
����ͳ��ͼ�����ش��������⣺
��1��ͳ�Ʊ��У�m���� ����n���� ����
��2������ͼ1�в�ȫ����ͳ��ͼ��
��3��������ͼ2��ʾ������ͳ��ͼ�У�D������������Ӧ��Բ�Ľ��Ƕ��ٶȣ�