题目内容
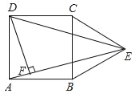
【题目】如图,在正方形ABCD的外侧,作等边三角形BCE,连接AE,DE.
(1)求证:AE=DE
(2)过点D作DF⊥AE,垂足为F,若AB=2cm,求DF的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)证明△ABE≌△DCE,可得结论;
(2)作辅助线,构建直角三角形,根据等腰三角形的性质得∠BCG=30°,∠DEF=30°,利用正方形的边长计算DE的长,从而得DF的长.
(1)证明:∵四边形ABCD是正方形,
∴AB=CD,∠ABC=∠DCB=90°,
∵△BCE是等边三角形,
∴BE=CE,∠EBC=∠ECB=60°,
即∠ABE=∠DCE=150°,
∴△ABE≌△DCE,
∴AE=DE;
(2)解:过点E作EG⊥CD于G,
∵DC=CE,∠DCE=150°,
∴∠CDE=∠CED=15°,
∴∠ECG=30°,
∵CB=CD=AB=2,
∴EG=1,CG=![]() ,
,
在Rt△DGE中,DE=![]() ,
,
在Rt△DEF中,∠EDA=∠DAE=90°﹣15°=75°
∴∠DEF=30°,
∴DF=![]() DE=
DE=![]() (cm).
(cm).

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】张先生今年7月份第一个星期的星期五以每股(份)25元的价格买进某种金融理财产品共2000股(买入时免收手续费),该理财产品在第二个星期的五个交易日中,每股的涨跌情况如下表(表格中数据表示比前一交易日涨或跌多少元) (单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌额 |
|
|
|
|
|
(1)写出第二个星期每日每股理财产品的收盘价(即每日最后时刻的成交价);
(2)已知理财产品卖出时,交易所需收取千分之三的手续费,如果张先生在第二个星期的星期五交易结束前将全部产品卖出,他的收益情况如何?