题目内容
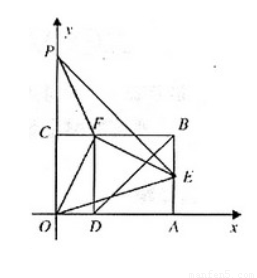
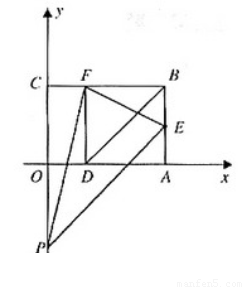
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处


1.直接写出点E、F的坐标;
2.设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
3.在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周 长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
【答案】
1. ;
;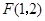
2.在 中,
中, ,
, .
.
设点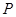 的坐标为
的坐标为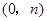 ,其中
,其中 ,∵顶点
,∵顶点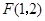 ,∴设抛物线解析式为
,∴设抛物线解析式为 .
.
① 如图①,
当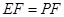 时,
时, ,
, .
.
解得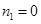 (舍去);
(舍去);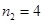 .
.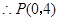 .
.
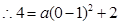 .解得
.解得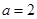 .
.
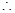 抛物线的解析式为
抛物线的解析式为 …………………………………………………2分
…………………………………………………2分
②如图②,
当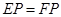 时,
时, ,
,
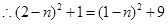 .
.
解得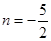 (舍去).…………………………………………………………………………………………2分
(舍去).…………………………………………………………………………………………2分
③当 时,
时,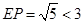 ,这种情况不存在.…………………………………1分
,这种情况不存在.…………………………………1分
综上所述,符合条件的抛物线解析式是
3.存在点 ,使得四边形
,使得四边形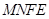 的周长最小.
的周长最小.
如图③,
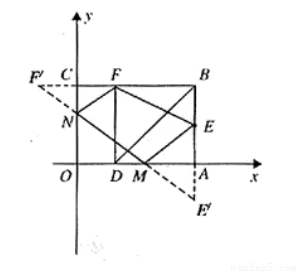
作点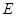 关于
关于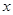 轴的对称点
轴的对称点 ,作点
,作点 关于
关于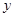 轴的对称点
轴的对称点 ,连接
,连接 ,分别与
,分别与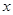 轴、
轴、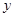 轴交于点
轴交于点 ,则点
,则点 就是所求点.……………………………………1分
就是所求点.……………………………………1分
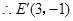 ,
,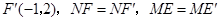 .
.
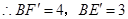 .
.
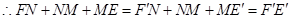
 .
.
又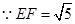 ,
, 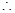
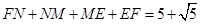 ,此时四边形
,此时四边形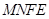 的周长最小值是
的周长最小值是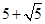 .……………………………………………………………………………………2分
.……………………………………………………………………………………2分
【解析】略

练习册系列答案
相关题目
 A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.
A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动. 10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为
10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为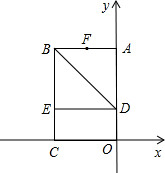 直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.
直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.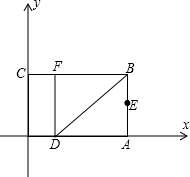 系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处. 如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.