题目内容
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=4cm,OC=3cm,D为OA上一动点,点D以1cm/s的速度从O点出发向 A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.
A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.(1)试写出多边形ODEBC的面积S(cm2)与运动时间t(s)之间的函数关系式;
(2)在(1)的条件下,当多边形ODEBC的面积最小时,在坐标轴上是否存在点P,使得△PDE为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)在某一时刻将△BED沿着BD翻折,使得点E恰好落在BC边的点F处.求出此时时间t的值.若此时在x轴上存在一点M,在y轴上存在一点N,使得四边形MNFE的周长最小,试求出此时点M,点N的坐标.
分析:(1)设OD=t,AD=4-t,AE=t,由S△DEBC=S△ABCD-S△DAE,列出关于t的函数,
(2)由(1)的一元二次方程求出最小值,分类P在x轴上时、在y轴上时求出满足条件的点,
(3)设AE=t,则BE=3-t.BF=BE=3-tAD=4-t,求出CF,然后求出t,解得M、N的坐标.
(2)由(1)的一元二次方程求出最小值,分类P在x轴上时、在y轴上时求出满足条件的点,
(3)设AE=t,则BE=3-t.BF=BE=3-tAD=4-t,求出CF,然后求出t,解得M、N的坐标.
解答:解:(1)设OD=t,AD=4-t,AE=t,
S△ODEBC=S△ABCD-S△DAE
=4×3-
AD•AE
=12-
(4-t)t
=
t2-2t+12(0≤t≤3)
(2)∵S=
t2-2t+12
∴-
=
=2
∴当t=2时,S有最小值;
此时:D(2,0)、E(4,2),
①当P在x轴上时,设P(a,0),
此时:DE2=AD2+EA2=22+22=8,
EP2=(a-4)2+22=a2-8a+20,
DP2=(a-2)2=a2-4a+4,
∴当DE2=EP2时,8=a2-8a+20,
∴a2-8a+12=0,
(a-2)(a-6)=0,
∴P(2,0),P1(6,0),
∵P(2,0)与D重合
∴舍去,
当EP2=DP2时,a2-8a+20=a2-4a+4,
16=4a,
a=4,
∴P2(4,0),
当DE2=DP2时,8=a2-4a+4a2-4a-4=0
a=
=2±2
,
∴P3(2+2
,0)P4(2-2
,0),
②当P在y轴上时,设P(0,b),
则DP2=22+b2=b2+4EP2=42+(b-2)2=16+b2-4b+4=b2-4b+20
DE2=8,
∴当DP2=EP2时,b2+4=b2-4b+20
4b=16,
b=4,
∴P5(0,4),
当EP2=DE2时,b2-4b+20=8b2-4b+12=0b2-4ac<0,
∴无解.
当DP2=DE2时,b2+4=8,
b2=4,
∴b=±2,
∴P6(0,-2)(DEP三点共线,舍去),
∴综上共有6个这样的P点,
使得△PDE为等腰三角形.
即P1(6,0),P2(4,0),P3(2+2
,0),P4(2-2
,0),P5(0,4),P6(0,2).
(3)设AE=t,则BE=3-t.BF=BE=3-t,AD=4-t,
∴CF=4-BF=t+1,
过D作DP⊥BC于P.
则:CP=OD=t,
∴PF=1,
又DP=3,
∴DF=
,
∴DE=DF=
,
∴在Rt△DAE中,AD2+AE2=DE2,
∴(4-t)2+t2=10,
∴t2-8t+16+t2=10,
2t2-8t+6=0,
t2-4t+3=0,
∴t1=1,t2=3(舍),
∴t=1(9分),
∴E(4,1),F(2,3),
∵E关于x轴的对称点E′(4,-1),F关于y轴的对称点F′(-2,3),
则E′F′与x轴,y轴的交点即为M点,N点.
设直线E′F′的解析式为y=kx+b(k≠0),
则
,
∴
,
∴y=-
x+
.(10分)
∴M(
,0),N(0,
).(12分)
S△ODEBC=S△ABCD-S△DAE
=4×3-
| 1 |
| 2 |
=12-
| 1 |
| 2 |
=
| 1 |
| 2 |
(2)∵S=
| 1 |
| 2 |
∴-
| b |
| 2a |
| -2 |
| 1 |
∴当t=2时,S有最小值;
此时:D(2,0)、E(4,2),
①当P在x轴上时,设P(a,0),
此时:DE2=AD2+EA2=22+22=8,
EP2=(a-4)2+22=a2-8a+20,
DP2=(a-2)2=a2-4a+4,
∴当DE2=EP2时,8=a2-8a+20,
∴a2-8a+12=0,
(a-2)(a-6)=0,
∴P(2,0),P1(6,0),
∵P(2,0)与D重合
∴舍去,
当EP2=DP2时,a2-8a+20=a2-4a+4,
16=4a,
a=4,
∴P2(4,0),
当DE2=DP2时,8=a2-4a+4a2-4a-4=0
a=
4±4
| ||
| 2 |
| 2 |
∴P3(2+2
| 2 |
| 2 |
②当P在y轴上时,设P(0,b),
则DP2=22+b2=b2+4EP2=42+(b-2)2=16+b2-4b+4=b2-4b+20
DE2=8,
∴当DP2=EP2时,b2+4=b2-4b+20
4b=16,
b=4,
∴P5(0,4),
当EP2=DE2时,b2-4b+20=8b2-4b+12=0b2-4ac<0,
∴无解.
当DP2=DE2时,b2+4=8,
b2=4,
∴b=±2,
∴P6(0,-2)(DEP三点共线,舍去),
∴综上共有6个这样的P点,
使得△PDE为等腰三角形.
即P1(6,0),P2(4,0),P3(2+2
| 2 |
| 2 |
(3)设AE=t,则BE=3-t.BF=BE=3-t,AD=4-t,
∴CF=4-BF=t+1,
过D作DP⊥BC于P.
则:CP=OD=t,
∴PF=1,
又DP=3,
∴DF=
| 10 |
∴DE=DF=
| 10 |
∴在Rt△DAE中,AD2+AE2=DE2,
∴(4-t)2+t2=10,
∴t2-8t+16+t2=10,
2t2-8t+6=0,
t2-4t+3=0,
∴t1=1,t2=3(舍),
∴t=1(9分),
∴E(4,1),F(2,3),
∵E关于x轴的对称点E′(4,-1),F关于y轴的对称点F′(-2,3),
则E′F′与x轴,y轴的交点即为M点,N点.
设直线E′F′的解析式为y=kx+b(k≠0),
则
|
∴
|
∴y=-
| 2 |
| 3 |
| 5 |
| 3 |
∴M(
| 5 |
| 2 |
| 5 |
| 3 |
点评:考查二次函数求最大(小)值的方法,综合面积的计算、勾股定理等内容,渗透分类讨论思想,综合性很强.

练习册系列答案
相关题目
 10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为
10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为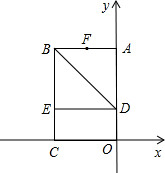 直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.
直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.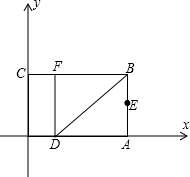 系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处. 如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.