题目内容
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标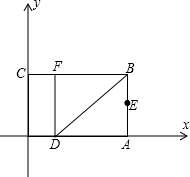 系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式.
分析:(1)由轴对称的性质,可知∠FBD=∠ABD,FB=AB,可得四边形ABFD是正方形,则可求点E、F的坐标;
(2)已知抛物线的顶点,则可用顶点式设抛物线的解析式.因为以点E、F、P为顶点的等腰三角形没有给明顶角的顶点,而顶角和底边都是惟一的,所以要抓住谁是顶角的顶点进行分类,可分别以E、F、P为顶角顶点进行分类计算.
(2)已知抛物线的顶点,则可用顶点式设抛物线的解析式.因为以点E、F、P为顶点的等腰三角形没有给明顶角的顶点,而顶角和底边都是惟一的,所以要抓住谁是顶角的顶点进行分类,可分别以E、F、P为顶角顶点进行分类计算.
解答: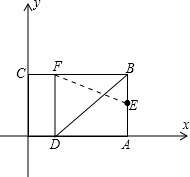 解:(1)E(3,1);F(1,2);
解:(1)E(3,1);F(1,2);
(2)连接EF,在Rt△EBF中,∠B=90°
∴EF=
=
,
设点P的坐标为(0,n),n>0,
∵顶点F(1,2),
∴设抛物线的解析式为y=a(x-1)2+2,(a≠0).
①当EF=PF时,EF2=PF2,
∴12+(n-2)2=5,
解得n1=0(舍去),n2=4.
∴P(0,4),
∴4=a(0-1)2+2,
解得a=2,
∴抛物线的解析式为y=2(x-1)2+2.
②当EP=FP时,EP2=FP2,
∴(2-n)2+1=(1-n)2+9,
解得n=-
(舍去).
③当EF=EP时,EP=
<3,这种情况不存在,
综上所述,符合条件的抛物线为y=2(x-1)2+2.
 解:(1)E(3,1);F(1,2);
解:(1)E(3,1);F(1,2);(2)连接EF,在Rt△EBF中,∠B=90°
∴EF=
| BE2+BF2 |
| 5 |
设点P的坐标为(0,n),n>0,
∵顶点F(1,2),
∴设抛物线的解析式为y=a(x-1)2+2,(a≠0).
①当EF=PF时,EF2=PF2,
∴12+(n-2)2=5,
解得n1=0(舍去),n2=4.
∴P(0,4),
∴4=a(0-1)2+2,
解得a=2,
∴抛物线的解析式为y=2(x-1)2+2.
②当EP=FP时,EP2=FP2,
∴(2-n)2+1=(1-n)2+9,
解得n=-
| 5 |
| 2 |
③当EF=EP时,EP=
| 5 |
综上所述,符合条件的抛物线为y=2(x-1)2+2.
点评:本题考查了矩形的性质,二次函数解析式的确定以及等腰三角形的构成情况等知识.
要注意(2)题在等腰三角形的腰和底不确定的情况下要分类讨论,不要漏解.
要注意(2)题在等腰三角形的腰和底不确定的情况下要分类讨论,不要漏解.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.
A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动. 10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为
10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为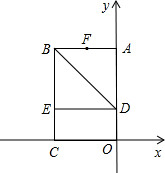 直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.
直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处. 如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.