题目内容
如图,以矩形OABC的顶点O为原点,OC所在的直线为x轴,OA所在的直线为y轴,建立平面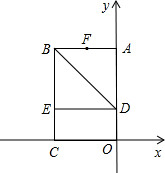 直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.
直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.(1)试判断四边形ABED的形状,并说明理由;
(2)若点F是AB的中点,设顶点为E的抛物线的右侧部分交x轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式.
分析:(1)∠BAE=90°,由折叠的性质可知∠ABD=∠EBD,得∠ABD=∠EBD=45°,可判断四边形ABED为正方形;
(2)连接EF,EO,通过计算可证△BEF≌△DEO,得出EF=EO,EF⊥EO,根据EF为腰和底两种情况,求抛物线解析式.
(2)连接EF,EO,通过计算可证△BEF≌△DEO,得出EF=EO,EF⊥EO,根据EF为腰和底两种情况,求抛物线解析式.
解答:解:(1)四边形ABED为正方形.
理由:由折叠的性质可知∠ABD=∠EBD,BA=BE,
又∵∠ABE=90°,
∴∠ABD=∠EBD=∠ADB=∠ABD=45°,
∴四边形ABED为正方形;
(2)连接EF,EO,依题意得顶点E(-4,2),
设抛物线解析式为y=a(x+4)2+2,
∵DO=AO-AD=OA-OC=2,BF=
AB=2,BE=DE,
∴△BEF≌△DEO,
∴EF=EO,EF⊥EO,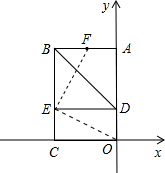
当EF为腰时,点P与点O重合,将P(0,0)代入y=a(x+4)2+2中,得a=-
,
∴y=-
(x+4)2+2,
当EF为底时,点P在EF的中垂线上,
∵E(-4,2),
∴直线OE解析式为y=-
x,
又∵EF⊥EO,线段EF的中点坐标为(-3,4),
∴EF的中垂线解析式为y=-
x+
,EF的中垂线与x轴交点P(5,0)
将P(5,0)代入y=a(x+4)2+2中,得a=-
,
∴y=-
(x+4)2+2,
∴抛物线解析式为y=-
(x+4)2+2或y=-
(x+4)2+2.
理由:由折叠的性质可知∠ABD=∠EBD,BA=BE,
又∵∠ABE=90°,
∴∠ABD=∠EBD=∠ADB=∠ABD=45°,
∴四边形ABED为正方形;
(2)连接EF,EO,依题意得顶点E(-4,2),
设抛物线解析式为y=a(x+4)2+2,
∵DO=AO-AD=OA-OC=2,BF=
| 1 |
| 2 |
∴△BEF≌△DEO,
∴EF=EO,EF⊥EO,

当EF为腰时,点P与点O重合,将P(0,0)代入y=a(x+4)2+2中,得a=-
| 1 |
| 8 |
∴y=-
| 1 |
| 8 |
当EF为底时,点P在EF的中垂线上,
∵E(-4,2),
∴直线OE解析式为y=-
| 1 |
| 2 |
又∵EF⊥EO,线段EF的中点坐标为(-3,4),
∴EF的中垂线解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
将P(5,0)代入y=a(x+4)2+2中,得a=-
| 2 |
| 81 |
∴y=-
| 2 |
| 81 |
∴抛物线解析式为y=-
| 1 |
| 8 |
| 2 |
| 81 |
点评:本题考查了二次函数的综合运用.关键是由折叠的性质判断正方形,确定相关点的坐标,根据EF为腰和底,分类求解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.
A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动. 10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为
10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为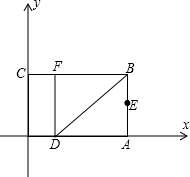 系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处. 如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.