题目内容
 如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.(Ⅰ)直接写出点E、F的坐标;
(Ⅱ)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M、N的坐标,并求出周长的最小值.
分析:(Ⅰ)△BDA沿BD翻折,使点A落在BC边上的点F处,可以知道四边形ADFB是正方形,因而BF=AB=OC=2,则CF=3-2=1,因而E、F的坐标就可以求出.
(Ⅱ)作点E关于x轴的对称点E′,作点F关于y轴的对称点F′,连接E′F′,分别与x轴、y轴交于点M,N,则点M,N就是所求点.
求出线段E′F′的长度,就是四边形MNFE的周长的最小值.
(Ⅱ)作点E关于x轴的对称点E′,作点F关于y轴的对称点F′,连接E′F′,分别与x轴、y轴交于点M,N,则点M,N就是所求点.
求出线段E′F′的长度,就是四边形MNFE的周长的最小值.
解答: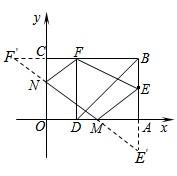 (本小题10分)
(本小题10分)
解:(Ⅰ)E(3,1);F(1,2).(2分)
(Ⅱ)如图,作点E关于x轴的对称点E′,
作点F关于y轴的对称点F′,连接E′F′,分别
与x轴、y轴交于点M、N,连接FN、NM、ME,
此时四边形MNFE的周长最小.(4分)
∴E′(3,-1),F′(-1,2),
设直线E′F′的解析式为y=kx+b,
有
解这个方程组,得
∴直线E′F′的解析式为y=-
x+
.
当y=0时,x=
,
∴M点的坐标为(
,0).
当x=0时,y=
,
∴N点的坐标为(0,
).(7分)
∵E与E′关于x轴对称,F与F′关于y轴对称,
∴NF=NF′,ME=ME′.F′B=4,E′B=3.
在Rt△BE′F′中,F′E′=
=
=5.
∴FN+NM+ME=F′N+NM+ME′=F′E′=5.
在Rt△BEF中,EF=
=
=
.
∴FN+NM+ME+EF=5+
,
即四边形MNFE的周长最小值是5+
.(10分)
 (本小题10分)
(本小题10分)解:(Ⅰ)E(3,1);F(1,2).(2分)
(Ⅱ)如图,作点E关于x轴的对称点E′,
作点F关于y轴的对称点F′,连接E′F′,分别
与x轴、y轴交于点M、N,连接FN、NM、ME,
此时四边形MNFE的周长最小.(4分)
∴E′(3,-1),F′(-1,2),
设直线E′F′的解析式为y=kx+b,
有
|
解这个方程组,得
|
∴直线E′F′的解析式为y=-
| 3 |
| 4 |
| 5 |
| 4 |
当y=0时,x=
| 5 |
| 3 |
∴M点的坐标为(
| 5 |
| 3 |
当x=0时,y=
| 5 |
| 4 |
∴N点的坐标为(0,
| 5 |
| 4 |
∵E与E′关于x轴对称,F与F′关于y轴对称,
∴NF=NF′,ME=ME′.F′B=4,E′B=3.
在Rt△BE′F′中,F′E′=
| F′B2+E′B2 |
| 42+32 |
∴FN+NM+ME=F′N+NM+ME′=F′E′=5.
在Rt△BEF中,EF=
| BE2+BF2 |
| 12+22 |
| 5 |
∴FN+NM+ME+EF=5+
| 5 |
即四边形MNFE的周长最小值是5+
| 5 |
点评:本题主要考查了待定系数法求函数解析式,求线段的和最小的问题基本的解决思路是根据对称转化为两点之间的距离的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.
A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动. 10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为
10、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为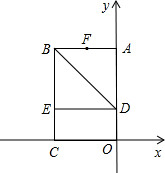 直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.
直角坐标系.已知OA=6,OC=4,在OA上取一点D,将△BDA沿BD翻折,点A恰好落在BC边上的点E处.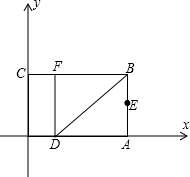 系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.