��Ŀ����
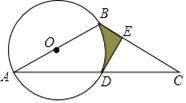
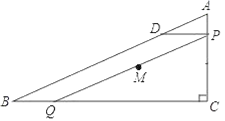
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8����P�ӵ�A�����ر�AC���C��ÿ��1����λ���ȵ��ٶ��˶���ͬʱ��Q�ӵ�C�����ر�CB���B��ÿ��a����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ��������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����a=2ʱ������������⣺
��QB=�� ����PD=�� �������ú�t�Ĵ���ʽ�ֱ��ʾ��
��ͨ������˵����������t��ֵʹ���ı���PDBQΪ���Σ�
��2����aΪij����ֵʱ���ı���PDBQ��ijһʱ��Ϊ���Σ���a��ֵ���ı���PDBQΪ����ʱt��ֵ��
��3����t=2ʱ���������˶������У�ǡ�ô����߶�PQ���е�M����ABC���߾�����ȣ�ֱ��д���˿�a��ֵ��
���𰸡���1����8��2t��![]() t���ڲ����ڣ����ɼ�������
t���ڲ����ڣ����ɼ�������
��2������![]() �룬�ı���PDBQ�����Σ�
�룬�ı���PDBQ�����Σ�
��3������������a��ֵΪ2��
�������������������1���ٸ�������ã�CQ=2t��PA=t����Rt��ABC�У���C=90�㣬AC=6��BC=8��PD��BC�����ɵ�tanA=![]() =
=![]() =
=![]() ��������QB��PD��ֵ��
��������QB��PD��ֵ��
������APD�ס�ACB���������AD��BD�ij�����BQ��DP���ɵõ�BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ�������ô�ʱDP��BD�ij�����DP��BD�����ж�PDBQ����Ϊ���Σ�
��2�����Q���ٶ�Ϊÿ��v����λ���ȣ���Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ���з��̼�����ô𰸣�
��3��������AP=2��PC=4��CQ=2a����QM=PM����M����ABC�����߾�����ȣ��Ƴ�CM�ǡ�PCQ��ƽ���ߣ��Ƴ�PC=CQ���ɵ�2a=4���Ƴ�a=2�������飬��ʱ��M����ABC�����ģ��ɴ˼��ɽ�����⣻
�����������1���ٸ�������ã�CQ=2t��PA=t��
��QB=8��2t��
����Rt��ABC�У���C=90�㣬AC=6��BC=8��PD��BC��
���APD=90�㣬
��tanA=![]() =
=![]() =
=![]() ��
��
��PD=![]() t��
t��
�ʴ�Ϊ����1��8��2t��![]() t��
t��
�ڲ�����
��Rt��ABC�У���C=90�㣬AC=6��BC=8��
��AB=10
��PD��BC��
���APD�ס�ACB��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��AD=![]() t��
t��
��BD=AB��AD=10��![]() t��
t��
��BQ��DP��
�൱BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ�
��8��2t=![]() ����ã�t=
����ã�t=![]() ��
��
��t=![]() ʱ��PD=
ʱ��PD=![]() ��
��![]() =
=![]() ��BD=10��
��BD=10��![]() ��
��![]() =6��
=6��
��DP��BD��
��PDBQ��������
��2�����Q���ٶ�Ϊÿ��v����λ���ȣ�
��BQ=8��vt��PD=![]() t��BD=10��
t��BD=10��![]() t��
t��
Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ��
��PD=BDʱ����![]() t=10��
t=10��![]() t����ã�t=
t����ã�t=![]() ��
��
��PD=BQ��t=![]() ʱ����
ʱ����![]() ��
��![]() =8��
=8��![]() v����ã�v=
v����ã�v=![]() ��
��
����Q���ٶ�Ϊÿ��![]() ����λ����ʱ������
����λ����ʱ������![]() �룬�ı���PDBQ�����Σ�
�룬�ı���PDBQ�����Σ�
��3��������AP=2��PC=4��CQ=2a��
��QM=PM����M����ABC�����߾�����ȣ�
��CM�ǡ�PCQ��ƽ���ߣ�
��PC=CQ��
��2a=4��
��a=2�������飬��ʱ��M����ABC�����ģ�
������������a��ֵΪ2��