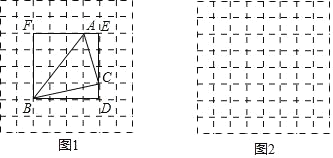题目内容
【题目】感知:如图①,在正方形![]() 中,
中,![]() 是
是![]() 一点,
一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,求证:
,求证:![]() ;
;
拓展:在图①中,若![]() 在
在![]() ,且
,且![]() ,则
,则![]() 成立吗?为什么?
成立吗?为什么?
运用:如图②在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)GE=BE+GD成立,理由见解析;(3)![]()
【解析】
(1)利用已知条件,可证出△BCE≌△DCF(SAS),即可得到CE=CF;
(2)借助(1)的结论得出∠BCE=∠DCF,再通过角的计算得出∠GCF=∠GCE,由SAS可得△ECG≌△FCG,则EG=GF,从而得出GE=DF+GD=BE+GD;
(3)过C作CG⊥AD,交AD延长线于G,先证四边形ABCG是正方形(有一组邻边相等的矩形是正方形),再设DE=x,利用(1)、(2)的结论,在Rt△AED中利用勾股定理构造方程即可求出DE.
(1)证明:如图①,在正方形ABCD中,BC=CD,∠B=∠ADC=90°,
∴∠CDF=90°,即∠B=∠CDF =90°,
在△BCE和△DCF中,
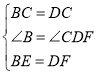 ,
,
∴△BCE≌△DCF(SAS),
∴CE=CF;
(2)解:如图①,GE=BE+GD成立,理由如下:
由(1)得△BCE≌△DCF,
∴∠BCE=∠DCF,
∴∠ECD+∠ECB=∠ECD+∠FCD,
即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠ECF∠ECG=45°,则∠GCF=∠GCE,
在△GEC和△GFC中,
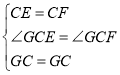 ,
,
∴△GEC≌△GFC(SAS),
∴EG=GF,
∴GE=DF+GD=BE+GD;
(3)解:如图②,过C作CG⊥AD于G,
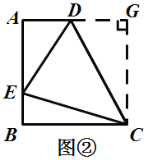
∴∠CGA=90°,
在四边形ABCD中,AD∥BC,∠A=∠B=90°,
∴四边形ABCG为矩形,
又∵AB=BC,
∴四边形ABCG为正方形,
∴AG=BC=AB=16,
∵∠DCE=45°,由(1)和(2)的结论可得:ED=BE+DG,
设DE=x,
∵![]() ,
,
∴AE=12,DG=x4,
∴AD=AGDG=20x
在Rt△AED中,
由勾股定理得:DE2=AD2+AE2,
即x2=(20x)2+122
解得:![]() ,
,
即![]() .
.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |

(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.