题目内容
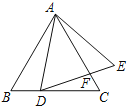
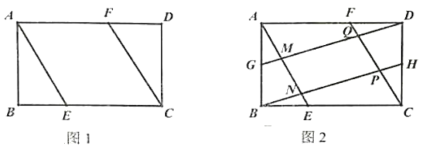
【题目】如图1,在矩形ABCD中AB=4, BC=8,点E、F是BC、AD上的点，且BE=DF.
(1)求证：四边形AECF是平行四边形.
(2)如果四边形AECF是菱形，求这个菱形的边长.
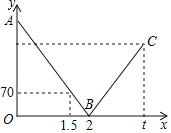
(3)如图2,在(2)的条件下，取AB、CD的中点G、H,连接DG、BH, DG分别交AE、CF于点M、Q, BH分别交AE、CF于点N、P,求点P到BC的距离并直接写出四边形MNPQ的面积。
【答案】（1）见解析；（2）菱形AECF的边长为5；（3）距离为
，面积为
【解析】
（1）根据矩形的性质可得AD∥BC，AD=BC，又BE=DF，所以AF∥EC，AF=EC，从而可得四边形AECF为平行四边形；
（2）设菱形AECF的边长为x，依据菱形的性质可得AE=EC=x，BE=8－x，在Rt△ABE中运用勾股定理可求解；
（3）先由中位线的性质得出CH=2，OH=1.5，再证明△PQH∽△PCB，根据相似三角形的性质得出h的w的值，再求出四边形MNPQ的面积即可.
（1）证明：∵四边形ABCD为矩形，BE=DF，
∴AD∥BC，AD=BC，
∴AF∥EC，AF=EC，
∴四边形AECF为平行四边形.
（2）解：设菱形AECF的边长为x，
∵四边形AECF为菱形，AB=4，BC=8，
∴AE=EC=x，BE=8－x，
在Rt△ABE中，AE2=AB2+BE2即x2=42+（8－x）2，
解得x=5，
∴菱形AECF的边长为5.
（3）连接GH交FC于点O，设点P到BC的距离为h，
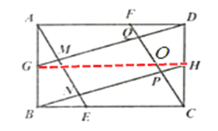
∵G、H分别为AB、CD的中点，
∴OH是△CDF的中位线，CH=2，
∴△POH∽△PCB，
∵DF=8－5=3，
∴QH=1.5，
∴
，解得h=，
由P到BC的距离可得N到BC的距离为
，四边形NECP的面积为
，菱形面积为5×4=20；
∴四边形MNPQ面积为=菱形AECF的面积-四边形NECP的面积×2=20-×2=
