题目内容
【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

【答案】(1)见解析; (2) 6.
【解析】
(1)设点P关于OM、ON对称点分别为P′、P″,当点A、B在P′P″上时,△PAB周长为PA+AB+BP=P′P″,此时周长最小.(2)根据轴对称的性质,可得△OP′P″是等边三角形即可解决问题.
(1)如图所示:
分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A.B,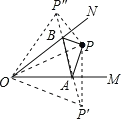
连接PA、PB,此时△PAB周长的最小值等于P′P″.
(2)如图所示:由轴对称性质可得,
OP′=OP″=OP=6cm,∠P′OA=∠POA,∠P″OB=∠POB,
所以∠P′OP″=2∠MON=2×30°=60°,
因为OP′=OP″,所以△OP″P′是等边三角形,
∴P′P″=6cm,
∴△APB的周长最小值为6cm,
故答案为6.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目