题目内容
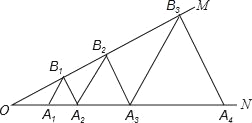
【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.
【答案】![]()
【解析】
首先由△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,∠MON=30°,求得A1B1=OA1=1,A2B2=OA2=OA1+A1A2=2,继而可得:△A3B3A4的边长为4,△A4B4A5的边长为8,则可得规律:△AnBnAn+1的边长为:2n-1;继而求得答案.
∵△A1B1A2是等边三角形,
∴∠B1A1A2=60°,
∴∠OB1A1=∠B1A1A2∠MON=30°,
∴∠OB1A1=∠MON,
∴A1B1=OA1=1,
∴△A1B1A2的边长为1,
同理:∠OB2A2=∠MON=30°,
∴A2B2=OA2=OA1+A1A2=2,
∴△A2B2A3的边长为2,
同理可得:△A3B3A4的边长为4,△A4B4A5的边长为8,
∴△AnBnAn+1的边长为:2n1;
∴△A2018B2018A2019的边长为:22017.
故答案为:22017.

练习册系列答案
相关题目