题目内容
【题目】如图，直线l1的函数关系式为
，且l1与x轴交于点D，直线l2经过定点A（4，0），B（﹣1，5），直线l1与l2相交于点C，
（1）求直线l2的解析式；
（2）求△ADC的面积；
（3）在直线l2上存在一点F（不与C重合），使得△ADF和△ADC的面积相等，请求出F点的坐标；
（4）在x轴上是否存在一点E，使得△BCE的周长最短？若存在请求出E点的坐标；若不存在，请说明理由．
【答案】（1）y=﹣x+4；（2）6；（3）（6，﹣2）；（4）见解析
【解析】
试题分析：（1）利用待定系数法即可直接求得l2的函数解析式；
（2）首先解两条之间的解析式组成的方程组求得C的坐标，然后利用三角形的面积公式即可求解；
（3）△ADF和△ADC的面积相等，则F的纵坐标与C的总坐标一定互为相反数，代入l2的解析式即可求解；
（4）求得C关于x轴的对称点，然后求得经过这个点和B点的直线解析式，直线与x轴的交点就是E．
解：（1）设l2的解析式是y=kx+b，
根据题意得：
，解得：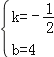
，
则函数的解析式是：y=﹣x+4；
（2）在
中令y=0，解得：x=﹣2，则D的坐标是（﹣2，0）．
解方程组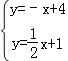
，
解得：
，
则C的坐标是（2，2）．
则S△ADC=
×6×2=6；
（3）把y=﹣2代入y=﹣x+4，得﹣2=﹣x+4，
解得：x=6，
则F的坐标是（6，﹣2）；
（4）C（2，2）关于x轴的对称点是（2，﹣2），
则设经过（2，﹣2）和B的函数解析式是y=mx+n，
则
，
解得：
，
则直线的解析式是y=3x+8．
令y=0，则3x+8=0，解得：x=﹣
．
则E的坐标是（﹣，0）．
练习册系列答案
阅读快车系列答案
相关题目
