题目内容
【题目】【问题提出】如图①,已知海岛A到海岸公路BD的距离为AB,C为公路BD上的酒店,从海岛A到酒店C,先乘船到登陆点D,船速为a,再乘汽车,车速为船速的n倍,点D选在何处时,所用时间最短?
【特例分析】若n=2,则时间t= ![]() +
+ ![]() ,当a为定值时,问题转化为:在BC上确定一点D,使得AD+
,当a为定值时,问题转化为:在BC上确定一点D,使得AD+ ![]() 的值最小.如图②,过点C做射线CM,使得∠BCM=30°.
的值最小.如图②,过点C做射线CM,使得∠BCM=30°.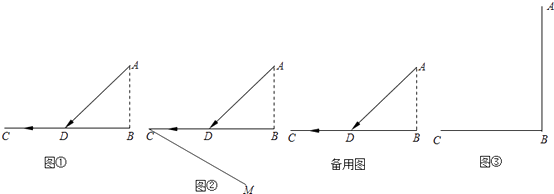
(1)过点D作DE⊥CM,垂足为E,试说明:DE= ![]() ;
;
(2)【问题解决】请在图②中画出所用时间最短的登陆点D′,并说明理由.
(3)【模型运用】请你仿照“特例分析”中的相关步骤,解决图①中的问题(写出具体方案,如相关图形呈现、图形中角所满足的条件、作图的方法等).
(4)如图③,海面上一标志A到海岸BC的距离AB=300m,BC=300m.救生员在C点处发现标志A处有人求救,
立刻前去营救,若救生员在岸上跑的速度都是6m/s,在海中游泳的速度都是2m/s,求救生员从C点出发到
达A处的最短时间.
【答案】
(1)解:如图①,
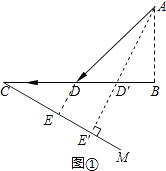
∵DE⊥CM,∴∠DEC=90°,
∴在Rt△BCM中,DE=CDsin30°,
∴DE= ![]() .
.
(2)解:如图①过点A作AE⊥CM交CB于点D',则D'点即为所用时间最短的登陆点.

理由如下:由第(1)问可知,D'E'= ![]() .
.
AD'+ ![]() 最短,即为AD'+D'E′最短.
最短,即为AD'+D'E′最短.
由直线外一点与这条直线上点的所有连线段中,垂线段最短.
可知此时D'点即为所求
(3)解:如图②,

过点C做射线CM,使得sin∠BCM= ![]() ,
,
过点A作AE⊥CM,垂足为E,交CB于点D,则D即为所用时间最短的登陆点.
(4)解:∵救生员在岸上跑的速度都是6m/s,在海中游泳的速度都是2m/s,
∴此时sin∠BCM= ![]() ,可得sin∠DAB=
,可得sin∠DAB= ![]() ,
,
∴在Rt△ADB中,AB=300,
AD=225 ![]() ,DB=75
,DB=75 ![]() ,CD=300﹣75
,CD=300﹣75 ![]() .
.
∴时间为 ![]() +
+ ![]() =(50+100
=(50+100 ![]() )s.
)s.
【解析】(1)在Rt△BCM中利用三角函数可求得;
(2)根据垂线段最短,可作出所用时间最短的登陆点D′;
(3)由“特例分析”可知n=2,则作∠BCM=30°,再仿照(2)的作法可得;
(4)由救生员在岸上跑的速度和在海中游泳的速度可求出sin∠BCM的值和sin∠DAB的值,在Rt△ADB中求出AD、BD,从而得到CD,从而可求得时间.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】学校为了丰富学生课余活动开展了一次“爱我云南,唱我云南”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70,9.60
B.9.60,9.60
C.9.60,9.70
D.9.65,9.60