题目内容
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.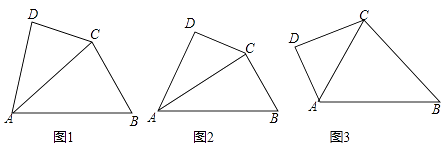
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
【答案】
(1)证明:∵∠DAB=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∴∠D+∠ACD=180°﹣30°=150°,
∵∠BCD=∠ACD+∠ACB=150°,
∴∠D=∠ACB,
∴△ADC∽△ACB.
∴AD:AC=AC:AB,
∴AC2=ABAD,
∴四边形ABCD为“可分四边形”;
(2)解:∵AC平分∠DAB,
∴∠DAC=∠BAC,
∵AC2=ABAD,
∴AD:AC=AC:AB,
∴△ADC∽△ACB,
∴∠D=∠ACB,
∵∠DCB=∠DAB,
∴∠DCB=∠DCA+∠ACB=2∠DAC,
∵∠DAC+∠D+∠ACB=180°,
∴∠DAC+2∠DAC=180°,
解得:∠DAC=60°,
∴∠DAB=120°;
(3)8
【解析】(3)∵四边形ABCD为“可分四边形”,AC=4,
∴ABAD=AC2=16,
当DA⊥DB时,△DAB的最大,最大面积为8,
所以答案是:8.
【考点精析】本题主要考查了勾股定理的概念和相似三角形的判定与性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】学校为了丰富学生课余活动开展了一次“爱我云南,唱我云南”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70,9.60
B.9.60,9.60
C.9.60,9.70
D.9.65,9.60