题目内容
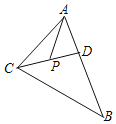
【题目】如图,在△ABC中,∠BAC=60°,D是AB上一点,AC=BD,P是CD中点.求证:AP=![]() BC.
BC.
【答案】详见解析.
【解析】
作辅助线,构建全等三角形和平行四边形,先证明四边形ACFD是平行四边形,得DF=AC=BD,DF∥AC,再证明△BDF是等边三角形,证明△ABC≌△BAF(SAS),可得结论.
证明:延长AP至点F,使得PF=AP,连结BF,DF,CF,
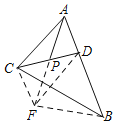
∵P是CD中点,
∴CP=DP,
∴四边形ACFD是平行四边形,
∴DF=AC=BD,DF∥AC,
∴∠FDB=∠BAC=60°,
∴△BDF是等边三角形,
∴BF=DF=AC,∠ABF=60°,
∴∠ABF=∠BAC,
在△ABC和△BAF中,
∵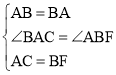 ,
,
∴△ABC≌△BAF(SAS),
∴AF=BC,
∴AP=![]() AF=
AF=![]() BC.
BC.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目