题目内容
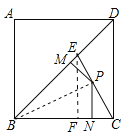
【题目】如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.

(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
【答案】(1)22.5°,(2)![]() .
.
【解析】
试题分析:(1)由正方形的性质得到,∠BCD=90°,∠DBC=45°,推出AB=BE,根据三角形的内角和定理求出∠BCE=∠BEC=67.5°,根据∠DCE=∠DCB-∠BCE即可求出答案.
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,得出△BEF是等腰直角三角形,从而求得BF=EF=![]() ,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
试题解析:(1)在正方形ABCD中,∠BCD=90°,∠DBC=45°,
∵BE=BC,
∴AB=BE,
∴∠BCE=∠BEC=![]() (180°-∠DBC)=67.5°,
(180°-∠DBC)=67.5°,
∴∠DCE=∠DCB-∠BCE=90°-67.5°=22.5°,
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,
∵∠EBF=45°,
∴△BEF是等腰直角三角形,
∵BE=BC=1,
∴BF=EF=![]() ,
,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
即![]() BEPM+
BEPM+![]() BCPN=
BCPN=![]() BCEF,
BCEF,
∵BE=BC,
∴PM+PN=EF=![]() .
.

【题目】某学校对学生的课外阅读时间进行抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如下的统计图表(图中信息不完整).
组别 | 阅读时间x(时) | 人数 |
A | 0≤x<10 | k |
B | 10≤x<20 | 100 |
C | 20≤x<30 | m |
D | 30≤x<40 | 140 |
E | x≥40 | n |

请结合以上信息解答下列问题
(1)阅读时间分组统计表中k、m、n的值分别是 、 、 ;
(2)补全“阅读人数分组统计图”;
(3)若全校有3000名学生,请估算全校课外阅读时间在20小时以下(不含20小时)的
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.