题目内容
【题目】如图,已知在平面直角坐标系中,![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,点C关于x轴的对称点为
,点C关于x轴的对称点为![]() ,
,![]() 是等腰直角三角形.
是等腰直角三角形.
![]() 的值等于______;
的值等于______;![]() 请直接写出
请直接写出![]()
![]() 把点A沿直线
把点A沿直线![]() 翻折,落在点
翻折,落在点![]() 的位置,如果点D在第一象限,
的位置,如果点D在第一象限,![]() 是以
是以![]() 为腰的等腰直角三角形,那么点D的坐标为______;
为腰的等腰直角三角形,那么点D的坐标为______;![]() 请直接写出
请直接写出![]()
![]() 求四边形
求四边形![]() 的面积.
的面积.

【答案】(1)3;(2)D(5,8)或(10,5);(3)20.
【解析】
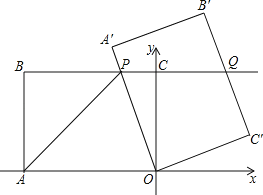
(1)如图,AB与CC'交于E,根据题意得 CB=BC',可知∠CBC'=90°,根据等腰直角三角形的性质可得BE=CE=3,可求m的值.
(2)根据对称性可求A'(7,0),分两类讨论,若∠DCA'=90°,过点D作DF⊥CE于F,可证△A'EC≌△DCF可得CF=5,DF=3,可得D的坐标,若∠DA'C=90°,同理可得.
(3)由图形可得SA'BCD=S△A'BC+S△A'CD,把具体数值代入即可.
(1)如图,AB与CC'交于E.
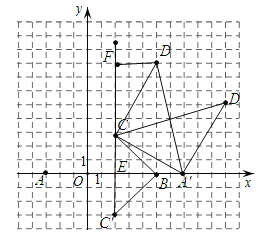
∵C与C'关于x轴对称,
∴BC=BC',BE⊥CC',
∴B是直角顶点,且△BCC'是等腰直角三角形,且BE⊥CC',
∴CE=C'E=BE.
∵B(5,0),C(2,m),∴BE=3=CE,
∴m=3;
(2)∵点A与点A'关于CC'对称,∴A'(7,0),∴A'E=5.
∵若∠DCA'=90°,且△A'CD是等腰直角三角形,∴DC=DA'.
过点D作DF⊥CE于F,
∴∠FDC+∠DCF=90°且∠ECA'+DCF=90°,
∴∠FDC=∠ECA'且A'C=DC,∠DFC=∠CEA'=90°,
∴△DCF≌CEA',
∴DF=CE=3,A'E=CF=5,
∴EF=8,
∴D(5,8).
若∠CA'D=90°,同理可得D(10,5),
∴D(5,8)或(10,5).
(3)∵AE=5,EC=3,∴A'C=![]() .
.
∵SA'BCD=S△A'BC+S△A'CD,
∴SA'BCD=![]() ×2×3+
×2×3+![]() ×
×![]() ×
×![]() =20.
=20.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图:
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;

(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?