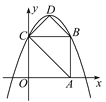题目内容
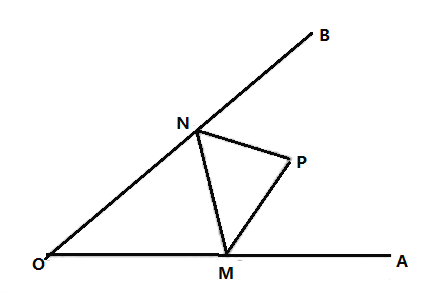
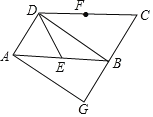
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF

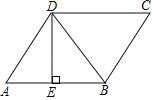
(1)如图1,当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
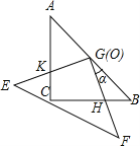
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为![]() ,对角线AE,DF相交于点O,连接OC.求OC的长度.
,对角线AE,DF相交于点O,连接OC.求OC的长度.
【答案】(1)证明见解析;(2)CF﹣CD=BC;(3)①CD﹣CF=BC;②2.
【解析】
(1)三角形ABC是等腰直角三角形,利用SAS即可证明△BAD≌△CAF,从而证得CF=BD,据此即可证得.
(2)同(1)相同,利用SAS即可证得△BAD≌△CAF,从而证得BD=CF,即可得到CF﹣CD=BC.
(3)①同(1)相同,利用SAS即可证得△BAD≌△CAF,从而证得BD=CF,即可得到CD﹣CB=CF.
②证明△BAD≌△CAF,△FCD是直角三角形,然后根据正方形的性质即可求得DF的长,则OC即可求得.
解:(1)∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°.∴AB=AC.
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°.
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,∴∠BAD=∠CAF.
∵在△BAD和△CAF中,AB=AC,∠BAD=∠CAF,AD=AF,
∴△BAD≌△CAF(SAS).∴BD=CF.
∵BD+CD=BC,∴CF+CD=BC.
(2)CF-CD=BC;
理由:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,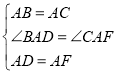 ,
,
∴△BAD≌△CAF(SAS)
∴BD=CF
∴BC+CD=CF,
∴CF-CD=BC;
(3)①∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠BAF,∠CAF=90°-∠BAF,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,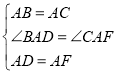 ,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∴CD-BC=CF,
②∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°.∴AB=AC.
∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°.
∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,∴∠BAD=∠CAF.
∵在△BAD和△CAF中,AB=AC,∠BAD=∠CAF,AD=AF,
∴△BAD≌△CAF(SAS).∴∠ACF=∠ABD.
∵∠ABC=45°,∴∠ABD=135°.∴∠ACF=∠ABD=135°.∴∠FCD=90°.
∴△FCD是直角三角形.
∵正方形ADEF的边长为![]() 且对角线AE、DF相交于点O,
且对角线AE、DF相交于点O,
∴DF=![]() AD=4,O为DF中点.
AD=4,O为DF中点.
∴OC=![]() DF=2.
DF=2.

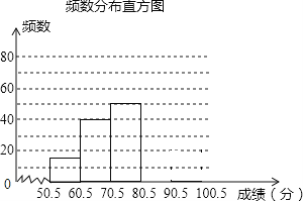
【题目】 某校为加强学生安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)进行统计,请根据尚为完成的频率和频数分布直方图,解答下列问题:
分数段 | 频数 | 频率 |
50.5~60.5 | 16 | 0.08 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 50 | 0.25 |
80.5~90.5 | m | 0.35 |
90.5~100.5 | 24 | n |
(1)这次抽取了______名学生的竞赛成绩进行统计,其中m=______,n=______;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?