题目内容
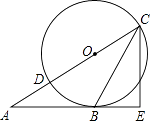
【题目】如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
A.线段AE的中垂线与线段AC的中垂线的交点
B.线段AB的中垂线与线段AC的中垂线的交点
C.线段AE的中垂线与线段BC的中垂线的交点
D.线段AB的中垂线与线段BC的中垂线的交点
【答案】C
【解析】解:连接AD,作AE的中垂线交AD于O,连接OE,
∵AB=AC,D是边BC的中点,
∴AD⊥BC.
∴AD是BC的中垂线,
∵BC是圆的切线,
∴AD必过圆心,
∵AE是圆的弦,
∴AE的中垂线必过圆心,
∴该圆的圆心是线段AE的中垂线与线段BC的中垂线的交点,故选C.
【考点精析】认真审题,首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等),还要掌握等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角))的相关知识才是答题的关键.

【题目】国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
类别 | 彩电 | 冰箱 | 洗衣机 |
进价(元/台) | 2000 | 1600 | 1000 |
售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
【题目】某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.
类别 | 频数 | 频率 |
助人为乐美德少年 | a | 0.20 |
自强自立美德少年 | 3 | b |
孝老爱亲美德少年 | 7 | 0.35 |
诚实守信美德少年 | 6 | 0.32 |
根据以上信息,解答下列问题:
(1)统计表中的a= ,b ;
(2)统计表后两行错误的数据是 ,该数据的正确值是 ;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率