Question

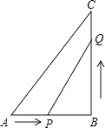
【题目】在等边△ABC中，AB＝5，点D是AB上的定点，点P是BC上的动点，DP绕点D逆时针旋转60°恰好落在AC上，已知BD＝2，则此时DP＝_____．

Answer 1

【答案】

【解析】

如图，连接PP'，过点D作DE⊥BC，由旋转的性质可证△DP'P是等边三角形，由“AAS”可证△BDP≌△CPP'，可得BD＝CP＝2，可求BP＝3，由直角三角形的性质和勾股定理可求DP的长．

解：如图，连接PP'，过点D作DE⊥BC，

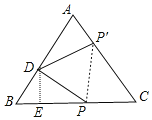
∵DP绕点D逆时针旋转60°，

∴DP＝DP'，∠PDP'＝60°，

∴△DP'P是等边三角形，

∴DP＝PP'，∠DPP'＝60°，

∵△ABC是等边三角形，

∴AB＝BC＝AC，∠A＝∠B＝∠C＝60°，

∵∠BPP'＝∠C+∠PP'C＝∠BPD+∠DPP'，

∴∠PP'C＝∠BPD，且DP＝PP'，∠B＝∠C，

∴△BDP≌△CPP'（AAS）

∴BD＝CP＝2，

∴BP＝3，

∵∠B＝60°，BD＝2，DE⊥BC，

∴BE＝1，，

∴PE＝2，

∴，

故答案为．