题目内容
【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
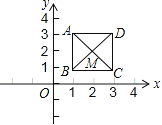
A.(-2012,2)B.(-2012,-2)C.(-2013,-2)D.(-2013,2)
【答案】A
【解析】
试题首先由正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),继而求得把正方形ABCD连续经过2014次这样的变换得到正方形ABCD的对角线交点M的坐标.
试题解析:∵正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).
∴对角线交点M的坐标为(2,2),
根据题意得:第1次变换后的点M的对应点的坐标为(2-1,-2),即(1,-2),
第2次变换后的点M的对应点的坐标为:(2-2,2),即(0,2),
第3次变换后的点M的对应点的坐标为(2-3,-2),即(-1,-2),
第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),
∴连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为(-2012,2).
故选A.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】某中学开展普通话演讲比赛,九(1)、(2)两个班根据初赛成绩各选出5名选手参加复赛,10名选手的复赛成绩如图所示:
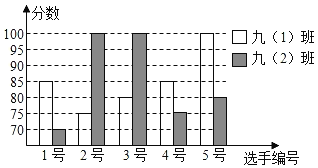
(1)根据如图补充完成下面的成绩统计分析表:
平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
九(1)班 | 85 |
| 85 |
|
| 60% |
九(2)班 | 85 | 80 |
| 160 | 100% |
|
(2)九(1)班学生说他们的复赛成绩好于九(2)班,结合图表,请你给出三条支持九(1)班学生观点的理由.
(3)如果从复赛成绩100分的3名选手中任选2人参加学校决赛,求选中的两位选手恰好一位来自于九(1)班,另一位来自于九(2)班的概率.