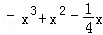Question

请看下面的问题：把x⁴+4分解因式
分析：这个二项式既无公因式可提，也不能直接利用公式，怎么办呢
19世纪的法国数学家苏菲•热门抓住了该式只有两项，而且属于平方和（x²）²+（2²）²的形式，要使用公式就必须添一项4x²，随即将此项4x²减去，即可得x⁴+4=x⁴+4x²+4﹣4x²=（x²+2）²﹣4x²=（x²+2）²﹣（2x）²=（x²+2x+2）（x²﹣2x+2）
人们为了纪念苏菲•热门给出这一解法，就把它叫做“热门定理”，请你依照苏菲•热门的做法，将下列各式因式分解．
（1）x⁴+4y⁴；（2）x²﹣2ax﹣b²﹣2ab．

Answer 1

（1）（x²+2y²+2xy）（x²+2y²﹣2xy） （2）（x+b）（x﹣2a﹣b）

试题分析：这是要运用添项法因式分解，首先要看明白例题才可以尝试做以下题目．
解：（1）x⁴+4y⁴=x⁴+4x²y²+4y²﹣4x²y²，
=（x²+2y²）²﹣4x²y²，
=（x²+2y²+2xy）（x²+2y²﹣2xy）；
（2）x²﹣2ax﹣b²﹣2ab，
=x²﹣2ax+a²﹣a²﹣b²﹣2ab，
=（x﹣a）²﹣（a+b）²，
=（x﹣a+a+b）（x﹣a﹣a﹣b），
=（x+b）（x﹣2a﹣b）．
点评：本题考查了添项法因式分解，难度比较大．