题目内容
如果一个三角形的三边长分别为1、k、4.则化简|2k-5|-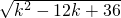 的结果是
的结果是
- A.3k-11
- B.k+1
- C.1
- D.11-3k
A
分析:由于三角形的三边长分别为1、k、4,根据三角形的三边关系,1+4>k,即k<5,4-1<k,所以k>3,根据k的取值范围,再对代数式进行化简.
解答:∵三角形的三边长分别为1、k、4,
∴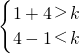 ,
,
解得,3<k<5,
所以,2k-5>0,k-6<0,
∴|2k-5|-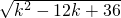 =2k-5-
=2k-5-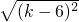 =2k-5-[-(k-6)]=3k-11.
=2k-5-[-(k-6)]=3k-11.
故选A.
点评:化简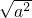 ,要根据二次根式的性质,先将
,要根据二次根式的性质,先将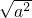 化为|a|,然后根据a的符号,去绝对值符号进行化简.
化为|a|,然后根据a的符号,去绝对值符号进行化简.
分析:由于三角形的三边长分别为1、k、4,根据三角形的三边关系,1+4>k,即k<5,4-1<k,所以k>3,根据k的取值范围,再对代数式进行化简.
解答:∵三角形的三边长分别为1、k、4,
∴
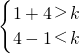 ,
,解得,3<k<5,
所以,2k-5>0,k-6<0,
∴|2k-5|-
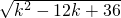 =2k-5-
=2k-5-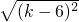 =2k-5-[-(k-6)]=3k-11.
=2k-5-[-(k-6)]=3k-11.故选A.
点评:化简
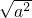 ,要根据二次根式的性质,先将
,要根据二次根式的性质,先将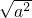 化为|a|,然后根据a的符号,去绝对值符号进行化简.
化为|a|,然后根据a的符号,去绝对值符号进行化简. 
练习册系列答案
相关题目
如果一个三角形的三边长分别为1、k、4.则化简|2k-5|-
的结果是( )
| k2-12k+36 |
| A、3k-11 | B、k+1 |
| C、1 | D、11-3k |
如果一个三角形的三边长分别为1,k,3,则化简7-
-|2k-3|的结果是( )
| 4k2-36k+81 |
| A、-5 | B、1 |
| C、13 | D、19-4k |
 【阅读理解】
【阅读理解】