题目内容
【题目】如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB交y轴于F点.
(1)求点A、B的坐标;
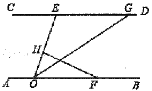
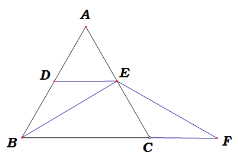
(2)点D为y轴正半轴上一点,若ED∥AB,且AM,DM分别平分∠CAB,∠ODE,如图 2,求∠AMD的度数;
(3)如图 3,(也可以利用图 1)①求点F的坐标;②坐标轴上是否存在点P,使得△ABP和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

【答案】(1)A(﹣3,0),B(3,3);(2)45°;(3)(0,5)或(0,﹣2)或(﹣10,0).
【解析】
(1)根据非负数的性质可求出a和b,即可得到点A和B的坐标;
(2)由平行线的性质结合角平分线的定义可得则∠NDM-∠OAN=45°,再利用∠OAN=90°-∠ANO=90°-∠DNM,得到∠NDM-(90°-∠DNM)=45°,所以∠NDM+∠DNM=135°,然后根据三角形内角和定理得180°-∠NMD=135°,可求得∠NMD=45°;
(3)①连结OB,如图3,设F(0,t),根据S△AOF+S△BOF=S△AOB,得到关于t的方程,可求得t的值,则可求得点F的坐标;②先计算△ABC的面积,再分点P在y轴上和在x轴上讨论.当P点在y轴上时,设P(0,y),利用S△ABP=S△APF+S△BPF,可解得y的值,可求得P点坐标;当P点在x轴上时,设P(x,0),根据三角形面积公式得,同理可得到关于x的方程,可求得x的值,可求得P点坐标.
(1)∵(a+b)2+|a﹣b+6|=0, ∴a+b=0,a﹣b+6=0,
∴a=﹣3,b=3, ∴A(﹣3,0),B(3,3);
(2)如图2,

∵AB∥DE,∴∠ODE+∠DFB=180°,
而∠DFB=∠AFO=90°﹣∠FAO,
∴∠ODE+90°﹣∠FAO=180°,
∵AM,DM分别平分∠CAB,∠ODE,
∴∠OAN=![]() ∠FAO,∠NDM=
∠FAO,∠NDM=![]() ∠ODE,
∠ODE,
∴∠NDM﹣∠OAN=45°,
而∠OAN=90°﹣∠ANO=90°﹣∠DNM,
∴∠NDM﹣(90°﹣∠DNM)=45°,
∴∠NDM+∠DNM=135°,∴180°﹣∠NMD=135°,
∴∠NMD=45°, 即∠AMD=45°;
(3)①连结OB,如图3,
设F(0,t),∵S△AOF+S△BOF=S△AOB,
∴![]() 3t+
3t+![]() t3=
t3=![]() ×3×3,解得t=
×3×3,解得t=![]() ,
,
∴F点坐标为(0,![]() );
);
②存在.
△ABC的面积=![]() ×7×3=
×7×3=![]() ,
,
当P点在y轴上时,设P(0,y),
∵S△ABP=S△APF+S△BPF,
∴![]() |y﹣
|y﹣![]() |3+
|3+![]() |y﹣
|y﹣![]() |3=
|3=![]() ,解得y=5或y=﹣2,
,解得y=5或y=﹣2,
∴此时P点坐标为(0,5)或(0,﹣2);
当P点在x轴上时,设P(x,0),
则![]() |x+3|3=
|x+3|3=![]() ,解得x=﹣10或x=4,
,解得x=﹣10或x=4,
∴此时P点坐标为(﹣10,0),
综上可知存在满足条件的点P,其坐标为(0,5)或(0,﹣2)或(﹣10,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案