题目内容
【题目】如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
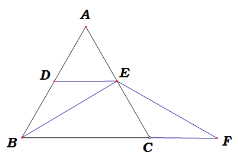

图1 图2
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
【答案】(1)证明见解析;(2)结论仍然成立;(3)
【解析】
(1)利用等边三角形的性质以及三线合一证明得出结论;
(2)由中位线的性质、平行线的性质,等边三角形的性质以及三角形全等的判定与性质证明
(1)证明:∵ΔABC是等边三角形,
∴∠ABC=∠ACB=![]() ,AB=BC=AC
,AB=BC=AC
∵DE是中位线,
∴E是AC的中点,
∴BE平分∠ABC,AE=EC
∴∠EBC=![]() ∠ABC=
∠ABC=![]()
∵AE=CF,
∴CE=CF,
∴∠CEF=∠F
∵∠CEF+∠F=∠ACB=![]() ,
,
∴∠F=![]() ,
,
∴∠EBC=∠F,
∴BE=EF
(2)结论仍然成立.
∵DE是由中位线平移所得;
∴DE//BC,
∴∠ADE=∠ABC=![]() ,∠AED=∠ACB=
,∠AED=∠ACB=![]() ,
,
∴ΔADE是等边三角形,
∴DE=AD=AE,
∵AB=AC,
∴BD=CE,
∵AE=CF,
∴DE=CF
∵∠BDE=![]() -∠ADE=
-∠ADE=![]() ,∠FCE=
,∠FCE=![]() -∠ACB=
-∠ACB=![]() ,
,
∴∠FCE=∠EDB,
∴ΔBDE≌ΔECF,
∴BE=EF

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.
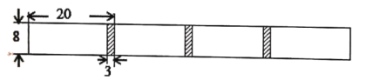
(1)根据题意,将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?