Question

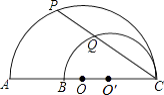
【题目】如图，△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形，则它们的面积比为（ ）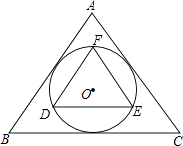
A.4
B.2
C.
D.

Answer 1

【答案】A
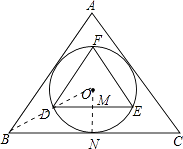
【解析】解：过点O作ON⊥BC垂足为N，交DE于点M，连接OB，则O，D，B三点一定共线，

设OM=1，则OD=ON=2，

∵∠ODM=∠OBN=30°，

∴OB=4，DM= ，DE=2 ，BN=2 ，BC=4 ，

∴S△ABC= ×4 ×6=12 ，

∴S△DEF= ×2 ×3=3 ，

∴ = =4．

故选A．

【考点精析】本题主要考查了正多边形和圆的相关知识点，需要掌握圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等才能正确解答此题．