题目内容
【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
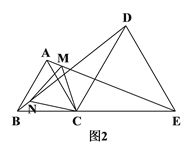
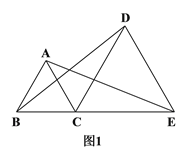
【答案】(1)证明见解析;(2)等边三角形,理由见解析.
【解析】试题分析:(1)由等边三角形的性质,可证明△DCB≌△ACE,可得到BD=AE;
(2)结合(1)中△DCB≌△ACE,可证明△ACM≌△BCN,进一步可得到∠MCN=60°且CM=CN,可判断△CMN为等边三角形.
试题解析:(1)∵△ABC、△DCE均是等边三角形,
∴AC=BC,DC=DE,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,
在△DCB和△ACE中,∵AC=BC,∠BCD =∠ACE, DC=DE,∴△DCB≌△ACE(SAS),∴BD=AE;
(2)△CMN为等边三角形,理由如下:由(1)可知:△ACE≌△DCB,
∴∠CAE=∠CDB,即∠CAM=∠CBN,
∵AC=BC,AM=BN,
在△ACM和△BCN中,∵AC=BC,∠CAM=∠CBN,AM=BN,∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
∵∠ACB=60°即∠BCN+∠ACN=60°,∴∠ACM+∠ACN=60°即∠MCN=60°,∴△CMN为等边三角形.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目



