题目内容
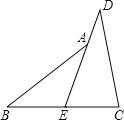
【题目】如图,在△ABC中,CA=CB,∠ABC=72°,BD是高线,BE是角平分线,若AB=12cm,则CE=_______cm,则∠DBE=_____度.

【答案】12 18
【解析】
利用等腰三角形的性质和角平分线的性质进行计算即可;
∵CA=CB,∠ABC=72°,
∴∠ACB=180°-2×72°=36°,
∵BE是角平分线,
∴∠EBC=![]() ∠ABC=36°,
∠ABC=36°,
∴三角形EBC为等腰三角形,
∴∠BEC=180°-36°-36°=108°,
∴∠BED=180°-108°=72°,
∵BD是高线,
∴∠BDE=90°,
∴∠DBE=180°-90°-72°=18°,
∴∠ABD=72°-18°-36°=18°,
∴△BDA≌△BDE(ASA)
∴AB=BE,
又∵三角形EBC为等腰三角形,
∴AB=CE=12cm.
故答案为:12,18.

练习册系列答案
相关题目