Question

【题目】如图，在△ABC中，AB=5，AC=12，BC=13，△ABD、△ACE、△BCF都是等边三角形，则四边形AEFD的面积S=__________.

Answer 1

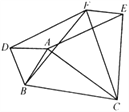
【答案】30

【解析】∵△ABD，△ACE都是等边三角形，

∴∠DAB=∠EAC=60°，

∵∠BAC=105°，

∴∠DAE=135°，

∵△ABD和△FBC都是等边三角形，

∴∠DBF+∠FBA=∠ABC+∠ABF=60°，

∴∠DBF=∠ABC.

在△ABC与△DBF中，

，

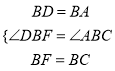∴△ABC≌△DBF(SAS)，

∴AC=DF=AE=12，

同理可证△ABC≌△EFC，

∴AB=EF=AD=5，

∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).

∴∠FDA=180°∠DAE=30°，

∴SAEFD=AD(DFsin45°)=5×(12×)=30.

即四边形AEFD的面积是30，

故答案为：30.

点睛:本题综合考查了勾股定理得逆定理,平行四边形的判定与性质,全等三角形的判定与性质以及等边三角形的性质,综合性比较强,难度较大,有利于培养学生综合运用知识进行推理和计算的能力.