Question

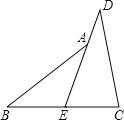
【题目】如图，E是BC的中点，点A在DE上，且∠BAE＝∠CDE.

求证：AB＝CD .

Answer 1

【答案】见解析

【解析】

此题要证明AB=CD，不能通过证明△ABE和△CED全等得到，因为根据已知条件无法证明它们全等；那么可以利用等腰三角形的性质来解题，为此必须把AB和CD通过作辅助线转化到一个等腰三角形中，而延长DE到F，使EF=DE，连接BF就可以达到要求，然后利用全等三角形的判定与性质就可以证明题目的问题．

证明：延长DE至点F，使EF＝DE，连接BF.

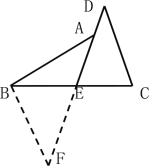
∵E是BC的中点

∴BE＝CE

在△BEF和△CED中

∴△BEF≌△CED

∴∠BFE＝∠CDE，BF＝CD

又∵∠BAE＝∠CDE

∴∠BFE＝∠BAE

∴AB＝BF

又∵BF=CD，

∴AB＝CD