题目内容
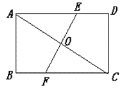
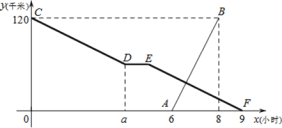
【题目】甲、乙两地相距 120 千米,小张骑自行车从甲地出发匀速驶往乙地,出发 a小时开始休息,1 小时后仍按原速继续行驶.小李比小张晚出发一段时间,骑摩托车从乙地匀速驶往甲地,图中折线 CD-DE-EF,线段 AB 分别表示小张、小李与乙地的距离 y(千米)与小张出发时间 x(小时)之间的函数关系图象.
(1)小李到达甲地后,再经过 小时小张到达乙地;小张骑自行车的速度是 千米/时;
(2)当 a=4 时,求小张与乙地的距离 y乙 与小张出发的时间 x(小时)之间的函数关系式;
(3)若小张恰好在休息期间与小李相遇,请直接写出 a 的取值范围.
【答案】(1)1,15;(2)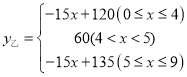 ;(3)
;(3)![]()
【解析】
(1)根据函数图象的横轴计算即可得解;根据速度=路程÷时间,计算即可得解;
(2)利用待定系数法求一次函数解析式求出EF、AB的解析式,然后分小张在小李的前方和小李在小张的前方分别列式计算即可得解;
(3)设小张出发![]() 小时与小李两人相遇,然后列出方程计算并用
小时与小李两人相遇,然后列出方程计算并用![]() 表示出
表示出![]() ,再根据
,再根据![]() 与
与![]() 的差在0到1之间列出不等式组求解即可.
的差在0到1之间列出不等式组求解即可.
(1)9-8=1(小时),小李到达甲地后,再经过1小时小张到达乙地;
![]() (千米/小时),小张骑自行车的速度是15千米/小时;
(千米/小时),小张骑自行车的速度是15千米/小时;
故答案为:1,15;
(2)根据题意得:D(4,60),E(5,60),F(9,0),
设线段EF的函数关系是为![]() ,
,
把E(5,60)和F(9,0)代入得 ,解得
,解得 ,
,
∴![]() ;
;
设线段CD的解析式为![]() ,把D(4,60)代入得:
,把D(4,60)代入得:![]() ,解得
,解得![]() ,
,
∴线段CD的解析式为![]() ,
,
∴当![]() 时,求小张与乙地的距离
时,求小张与乙地的距离![]() 与小张出发的时间
与小张出发的时间![]() (小时)之间的函数关系式为:
(小时)之间的函数关系式为:
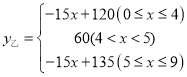 ;
;
(3)设小张出发![]() 小时与小李两人相遇,
小时与小李两人相遇,
小李骑摩托车的速度是:![]() (千米/小时),
(千米/小时),
根据题意得,![]() ,
,
整理得,![]() ,
,
∵小张恰好在休息期间与小李相遇,
∴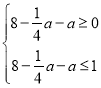 ,
,
解不等式![]() 得:
得:![]() ,
,
解不等式![]() 得:
得:![]() ,
,
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案