题目内容
【题目】已知,AB是⊙O的直径,BC是弦,直线CD是⊙O的切线,切点为C,BD⊥CD.
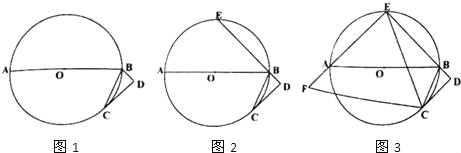
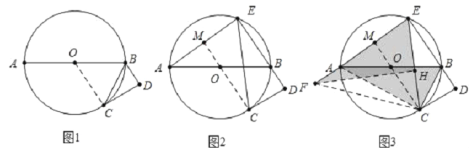
(1)如图1,求证:BC平分∠ABD;
(2)如图2,延长DB交⊙O于点E,求证:弧AC =弧EC;
(3)如图3,在(2)的条件下,连接EA并延长至F,使EF=AB,连接CF、CE,若tan∠FCE=![]() ,BC=5,求AF的长.
,BC=5,求AF的长.
【答案】(1)详见解析;(2)详见解析;(3)AF=EF﹣AE=![]() .
.
【解析】
试题分析:(1)如图1中,欲证明BC平分∠ABD,只要证明∠CBD=∠CBO,只要证明BD∥OC即可.(2)如图2中,连接AE,连接CO并延长交AE于M欲证明弧AC =弧EC,只要证明CM⊥AE即可.(3)如图3中,连接AC,连接CO并延长交AE于M,过F作FH⊥CE于H,首先证明△FHE≌△ACB,根据tan∠FCE=![]() ,设FH=12k,CH=7k,列出方程求出k,通过解直角三角形分别求出EF、AE即可解决问题.
,设FH=12k,CH=7k,列出方程求出k,通过解直角三角形分别求出EF、AE即可解决问题.
试题解析:(1)证明:如图1中,连接OC,
∵AB是⊙O直径,DC是⊙O切线,
∴OC⊥CD,
∴∠OCD=90°,∵BD⊥CD,∴∠D=90°,
∴∠OCD+∠D=180°,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OB=OC,
∴∠OCB=∠OBC,
∴∠OBC=∠CBD,
∴BC平分∠OBD.
(2)证明:如图2中,连接AE,连接CO并延长交AE于M.
∵AB是直径,
∴∠AEB=90°,
∵CM∥DB,
∴∠AMC=∠AEB=90°,
∴CM⊥AB,
∴∠AMC=∠AEB=90°,
∴CM⊥AB,且CM经过圆心O,
∴弧AC =弧EC.
(3)解:如图3中,连接AC,连接CO并延长交AE于M,过F作FH⊥CE于H,
∵FH⊥CE,
∴∠FHE=∠FHC=90°,
由(2)可知∠AMC=90°,
∴∠CME=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠FHE=∠ACB=90°,
∵FH=AB,∠FEH=∠ABC,
∴△FHE≌△ACB,
∴FH=AC,EH=BC,
在RT△FHC中,tan∠FCE=![]() ,设FH=12k,CH=7k,
,设FH=12k,CH=7k,
∴FH=AC=12k,
∵弧AC =弧EC,
∴CE=AC=12k,
∴EH=BC=5k,
∵BC=5,
∴5k=5,
∴k=1,∴AC=12,
在RT△ACB中,AB=![]() =13,∴AB=EF=13,
=13,∴AB=EF=13,
在RT△ACB中,sin∠ABC=![]() ,∵∠ABC=∠CBD,
,∵∠ABC=∠CBD,
在RT△CBD中,sin∠CBD=![]() ,∴CD=
,∴CD=![]() ,
,
∵∠AED=∠D=∠ACB=90°,
∴四边形CMED是矩形,
∴CD=ME=![]() ,
,
∴AM=ME,
∴AE=2ME=![]() ,
,
∴AF=EF﹣AE=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】郑州市雾霾天气趋于严重,丹尼斯商场根据民众健康需要,代理销售每台 进价分别为600元、560元的A、B两种型号的空气净化器,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 4台 | 5台 | 7100元 |
第二周 | 6台 | 10台 | 12600元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的空气净化器的销售单价;
(2)若商场准备用不多于17200元的金额再采购这两种型号的空气净化器共30台,超市销售完这30台空气净化器能否实现利润为6200元的目标,若能,请给出相应的采购方案;若不能,请说明理由.