题目内容
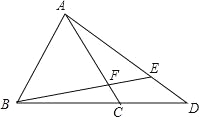
【题目】如图，△ABC是等边三角形，延长BC至D，连接AD，在AD上取一点E，连接BE交AC于F，若AF+CD=AD，DE=2，AF=4，则AD长为 ．
【答案】AD=7．
【解析】
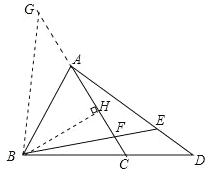
试题分析：如图，延长CA至点G使GA=CD，连接GB，
∵△ABC是等边三角形，
∴AB=CA，∠BAC=∠ACB=60°，
∴∠GAB=∠DCA=120°，
∴在△GBA与△DAC中，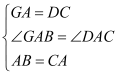
，
∴△GBA≌△DAC（SAS），
∴BG=AD，
∵AF+CD=AD，AF+GA=GF，
∴GF=AD，
∴BG=GF．
∴∠GBF=∠GFB．
又∵∠GBA=∠CAD，
∴∠ABE=∠AEB，
∴AB=AE．
设AD=a，则BG=a，AB=AE=a﹣2，GA=GF﹣AF=BG﹣AF=a﹣4，
又∵∠GAB=120°，
∴作BH⊥AC，垂足为H，易求a=7，即AD=7．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
