Question

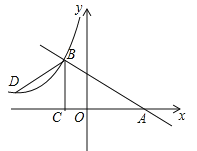
【题目】如图，在平面直角坐标系中，O为坐标原点，的边垂直于轴，垂足为B，反比例函数的图象经过AO上的点C，且，与边AB相交于点D, ．

（1）求点C的横坐标；

（2）求反比例函数的解析式；

（3）求经过C，D两点的一次函数解析式．

Answer 1

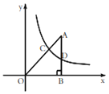
【答案】（1）点C的横坐标是4；（2）；（3）．

【解析】

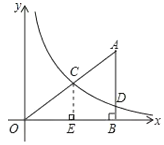
（1）过点C作CE⊥x轴于点E，利用平行线分线段成比例定理列出比例式，求出OE即可；

（2）设点D的坐标为（6，m）（m＞0），则点A的坐标为（6，＋m），由点A的坐标求出点C的坐标，根据点C、D在反比例函数图象上可得出关于m的方程，解方程求出m即可得出结论；

（3）由m的值，可得出点C、D的坐标，利用待定系数法即可得出结论．

解：（1）如图，过点C作CE⊥x轴于点E，

∵AB⊥x轴，

∴CE∥AB，

∴，即，

∴OE＝4，

∴点C的横坐标是4；

（2）设点D的坐标为（6，m）（m＞0），则点A的坐标为（6，＋m），

由（1）知，即，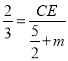

∴，

∴点C的坐标为（4，），

∵点C、点D均在反比例函数的函数图象上，

∴6m＝，

解得：m＝2，

∴k＝6m＝12，

∴反比例函数的解析式为；

（3）∵m＝2，

∴点C的坐标为（4，3），点D的坐标为（6，2），

设经过点C、D的一次函数的解析式为y＝ax＋b（a≠0），

则有，

解得：，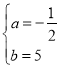

∴经过C、D两点的一次函数解析式为．