题目内容
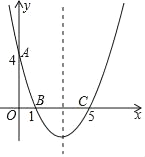
【题目】小聪对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为0或4时,函数值都为-3,当自变量
的值为0或4时,函数值都为-3,当自变量![]() 的值为-1或5时,函数值为2.
的值为-1或5时,函数值为2.
探究过程如下,请补充完整.
(1)这个函数的表达式为 ;
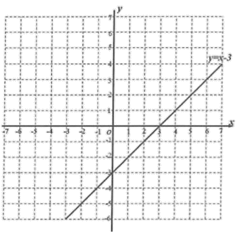
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的一条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有4个解,则k的取值范围为 ;
有4个解,则k的取值范围为 ;
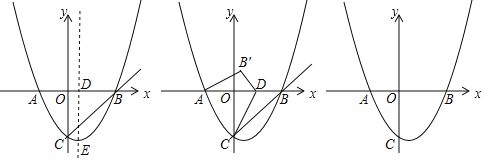
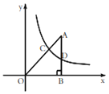
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]() 的解集: .
的解集: .
【答案】(1)![]() ;(2)函数图象关于直线
;(2)函数图象关于直线![]() 对称;(3)①
对称;(3)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)根据题意将![]() 四个点代入函数表达式用待定系数法求参数即可.
四个点代入函数表达式用待定系数法求参数即可.
(2)用描点法画出函数图象,观察图象,阐述其一条性质即可,如对称性,增减性.
(3)①直线![]() 平行于
平行于![]() 轴,作出这条直线并上下平移,即可找到符合要求的
轴,作出这条直线并上下平移,即可找到符合要求的![]() 的取值范围;②根据图象,找到相同
的取值范围;②根据图象,找到相同![]() 值分别对应的
值分别对应的![]() 的值与
的值与![]() 值中一次函数较大或者相等的部分.
值中一次函数较大或者相等的部分.
解:(1)根据题意将![]() 代入
代入![]() 得,
得,

解得 .
.
故该函数表达式为![]() ;
;
(2)函数图象关于直线![]() 对称;(从数学角度叙述有理就行)
对称;(从数学角度叙述有理就行)
(3)①直线![]() 与函数
与函数![]() 有4个解,则两函数图象有4个交点,观察图象可得
有4个解,则两函数图象有4个交点,观察图象可得![]() ;
;
②不等式![]() 的解集表示函数
的解集表示函数![]() 的值小于或者等于
的值小于或者等于![]() 的值所对应的
的值所对应的![]() 的取值部分,观察图象可得,
的取值部分,观察图象可得,![]() 或
或![]() .
.


练习册系列答案
相关题目