题目内容
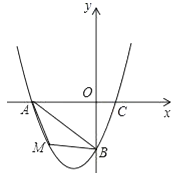
【题目】已知四边形ABCD是菱形，在平面直角坐标系中的位置如图，边AD经过原点O，已知A（0，﹣3），B（4，0），反比例函数图象经过点C，直线AC交双曲线另一支于点E，连接DE，CD，设反比例函数解析式为y1= 
，直线AC解析式为y2=ax+b．
（1）求反比例函数解析式；
（2）当y1＜y2时，求x的取值范围；
（3）求△CDE的面积．
【答案】
（1）解：∵A（0，﹣3），B（4，0），
∴AB= 
=5=BC，
∴C（4，5），
∵反比例函数y1= 
图象经过点C，
∴k=4×5=20，
∴反比例函数解析式为y1= 
（2）解：把A（0，﹣3），C（4，5）代入y2=ax+b得，
，解得 
直线AC解析式为y2=2x﹣3，
解 
得 
， 
，
∴E（﹣ 
，﹣8）
当y1＜y2时，x＞4或﹣ ＜x＜0
（3）解：S△CDE=S△ADE+S△ADC= 
×× 
+ ×5×4= 
【解析】抓住已知菱形四边形ABCD是菱形，AD在y轴上，得出CB⊥x轴，根据点A、B的坐标求出菱形的边长，就可以求出点C的坐标，用待定系数法就可以求出反比例函数的解析式。
（2）先求出直线AC的函数解析式，再求出交点E的坐标，观察被直线x=-、直线x=4,、y轴分得的四部分函数图像，即可得出1＜y2时，x的取值范围。
（3）根据S△CDE=S△ADE+S△ADC，根据三角形的面积公式即可求解。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对菱形的性质的理解，了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．
