题目内容
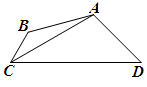
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒).

(1)当t=2时,求△BPQ的面积;
(2)若四边形ABQP为平行四边形,求运动时间t.
(3)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?

(1)当t=2时,求△BPQ的面积;
(2)若四边形ABQP为平行四边形,求运动时间t.
(3)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(1)84;(2)5;(3)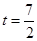 或
或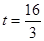
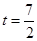 或
或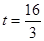
试题分析:(1)先求出t=2时BQ的长,再根据三角形的面积公式即可求得结果;
(2)根据平行四边形的判定方法可知只须AP=BQ,即可得到关于t的方程,解出即可;
(3)分三种情况:
(1)∵BQ=16-2=14,∴
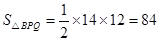 ;
; (2)只须AP=BQ,即
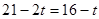 ,解得t=5;
,解得t=5;(3)下面分三种情况讨论:①以∠B为顶角时,BP=BQ,②以∠Q为顶角时,QB=QP,③以∠P为顶角时,PB=PQ,再根据等腰三角形的性质分析即可.
①以∠B为顶角时,BP=BQ,
有
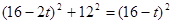 ,
,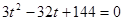 ,∵△<0 ∴无解
,∵△<0 ∴无解②以∠Q为顶角时,QB=QP,有:
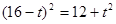 ,解得
,解得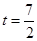
③以∠P为顶角时,PB=PQ,有:
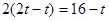 ,解得
,解得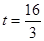
综上,
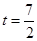 或
或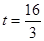 时,符合题意.
时,符合题意.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
 ,
, ,
,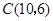 ,
, ,直线
,直线 将四边形
将四边形 分成面积相等的两部分,则
分成面积相等的两部分,则 的值为 .
的值为 . BFD.
BFD.
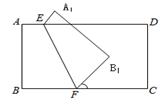
 ,正方形ABCD的边长为
,正方形ABCD的边长为 ,猜想
,猜想 的大小,并结合图3证明你的猜想.
的大小,并结合图3证明你的猜想. 
 中,
中,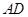 ∥
∥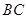 ,已知
,已知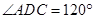 ,
,
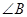 的度数;
的度数;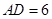 ,
,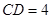 ,试求等腰梯形
,试求等腰梯形 中,
中, 是
是 边上的一点,
边上的一点,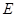 是
是 的中点,过点
的中点,过点 作
作 的延长线于
的延长线于 ,且
,且 ,连接
,连接 .
.
 ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.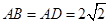 ,求四边形ABCD的面积.
,求四边形ABCD的面积.