题目内容
如图,在菱形ABCD中,点E是AB的中点,且DE⊥AB.

(1)求∠ABD的度数;
(2)若菱形的边长为2,求菱形的面积.

(1)求∠ABD的度数;
(2)若菱形的边长为2,求菱形的面积.
(1)60°;(2) .
.
 .
.试题分析:(1)根据菱形的性质可得到AD=BD,AD=AB,从而可推出△ABD是等边三角形,从而不难求得∠ABD的度数.
(2)根据勾股定理可求得DE的长,再根据菱形的面积公式即可求得菱形的面积.
试题解析:(1)∵DE⊥AB,AE=BE
∴△ABD是等腰三角形,
∴AD=BD
∵四边形ABCD是菱形
∴AD=AB
∴AD=AB=BD,
∴△ABD是等边三角形
∴∠ABD=60°
(2)∵AD=AB=2,
∴AE=1,
在Rt△AED中,DE=

∴S菱形ABCD=AB•DE=
 .
.
练习册系列答案
相关题目

 ,这是个 边形
,这是个 边形 时,则线段BH的长是 .
时,则线段BH的长是 .


 中,对角线
中,对角线 分别等于8和6,将
分别等于8和6,将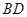 沿
沿 的方向平移,使
的方向平移,使 与
与 重合,
重合, 与
与 重合,则四边形
重合,则四边形 的面积等于( )
的面积等于( )