题目内容
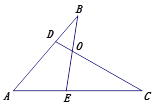
【题目】(1)已知:如图1,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点O,求证:∠BOC=90°+![]() ∠A;
∠A;
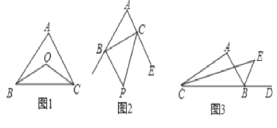
(2)如图2,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的平分线,试探究∠BPC与∠A的关系.
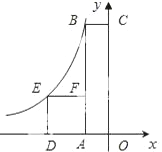
(3)如图3,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究∠BEC与∠A的关系.
【答案】(1)见解析;(2)∠BPC=90°![]() ∠A,理由见解析;(3)2∠BEC=∠A.
∠A,理由见解析;(3)2∠BEC=∠A.
【解析】
(1)先根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB,则2∠BOC=360°-2∠OBC-2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°-∠ABC-∠ACB,易得∠BOC=90°+![]() ∠A;
∠A;
(2)根据三角形外角平分线的性质可得∠BCP=![]() (∠A+∠ABC)、∠PBC=
(∠A+∠ABC)、∠PBC=![]() (∠A+∠ACB);根据三角形内角和定理可得∠BPC=90°-
(∠A+∠ACB);根据三角形内角和定理可得∠BPC=90°-![]() ∠A;
∠A;
(3)根据CE为∠ABC的角平分线,BE为△ABC外角∠ABD的平分线,可知,∠A=180°-∠1-∠3,∠E=180°-∠4-∠ABE=180°-∠3-![]() (∠A+2∠1),两式联立可得2∠BEC=∠A.
(∠A+2∠1),两式联立可得2∠BEC=∠A.
(1)证明:在△BOC中,
∵∠BOC=180°∠OBC∠OCB,
∴2∠BOC=360°2∠OBC2∠OCB,
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+![]() ∠A;
∠A;
(2)∠BPC=90°![]() ∠A.
∠A.
证明:∵BP、CP为△ABC两外角∠ABC、∠ACB的平分线,∠A为x°,
∴∠BCP=![]() (∠A+∠ABC)、∠PBC=
(∠A+∠ABC)、∠PBC=![]() (∠A+∠ACB),
(∠A+∠ACB),
由三角形内角和定理得,∠BPC=180°∠BCP∠PBC=180°![]() [∠A+(∠A+∠ABC+∠ACB)]=180°
[∠A+(∠A+∠ABC+∠ACB)]=180°![]() (∠A+180°)=90°
(∠A+180°)=90°![]() ∠A;
∠A;
(3)2∠BEC=∠A.
证明:∵CE为∠ACB的角平分线,BE为△ABC外角∠ABD的平分线,两角平分线交于点E,
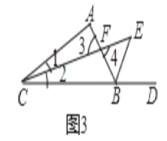
∴∠1=∠2,∠ABE=![]() (∠A+2∠1),∠3=∠4,
(∠A+2∠1),∠3=∠4,
在△ACF中,∠A=180°∠1∠3
∴∠1+∠3=180°∠A①
在△BEF中,∠E=180°∠4∠ABE=180°∠3![]() (∠A+2∠1),
(∠A+2∠1),
即2∠E=360°2∠3∠A2∠1=360°2(∠1+∠3)∠A②,
把①代入②得2∠E=∠A,即2∠BEC=∠A.

 名题金卷系列答案
名题金卷系列答案