Question

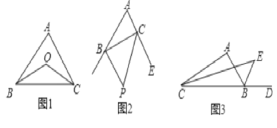
【题目】如图，点D在AB上，点E在AC上，BE、CD相交于点O.

（1）若∠A=50°，∠BOD=70°，∠C=30°，求∠B的度数；

（2）试猜想∠BOC与∠A+∠B+∠C之间的关系，并证明你猜想的正确性.

Answer 1

【答案】（1）30°；（2）∠BOC=∠A+∠B+∠C，理由见解析.

【解析】

（1）利用三角形外角的性质和三角形内角和定理即可求得∠B的度数；（2）用三角形外角和定理求出∠BOC，∠BEC的两角之和，最后得出结论.

解：（1）∵∠A=50°，∠C=30°，∴∠BDO=80°；∵∠BOD=70°，∴∠B=30°；

（2）∠BOC=∠A+∠B+∠C.

理由：∵∠BOC=∠BEC +∠C，∠BEC=∠A+∠B，

∴∠BOC=∠A+∠B+∠C.