题目内容
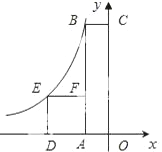
【题目】如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数![]() 的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为________.
的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为________.
【答案】-6
【解析】先由正方形ADEF的面积为4,得出边长为2,BF=2AF=4,AB=AF+BF=2+4=6,再设B点坐标为(t,6),则E点坐标(t-2,2),根据点B、E在反比例函数y=![]() 的图象上,利用根据反比例函数图象上点的坐标特征得k=6t=2(t-2),即可求出k=-6.
的图象上,利用根据反比例函数图象上点的坐标特征得k=6t=2(t-2),即可求出k=-6.
∵正方形ADEF的面积为4,
∴正方形ADEF的边长为2,
∴BF=2AF=4,AB=AF+BF=2+4=6,
设B点坐标为(t,6),则E点坐标(t-2,2),
∵点B、E在反比例函数y=![]() 的图象上,
的图象上,
∴k=6t=2(t-2),
解得t=-1,k=-6,
故答案为:-6.

练习册系列答案
相关题目