题目内容
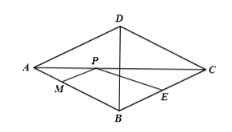
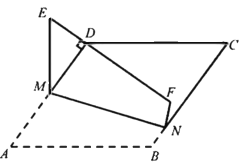
【题目】如图，在菱形
中，
，
分别在边
上，将四边形
沿
翻折，使
的对应线段
经过顶点
，当
时，
的值为__________.
【答案】
【解析】首先延长NF与DC交于点H，进而利用翻折变换的性质得出NH⊥DC，再利用边角关系得出BN，CN的长进而得出答案．
延长NF与DC交于点H，
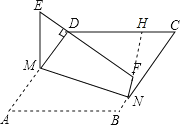
∵∠ADF=90°，
∴∠A+∠FDH=90°，
∵∠DFN+∠DFH=180°，∠A+∠B=180°，∠B=∠DFN，
∴∠A=∠DFH，
∴∠FDH+∠DFH=90°，
∴NH⊥DC，
设DM=4k，DE=3k，EM=5k，
∴AD=9k=DC，DF=6k，
∵tanA=tan∠DFH=
，
则sin∠DFH=
，
∴DH=DF=
k，
∴CH=9k-k=
k，
∵cosC=cosA=
，
∴CN=
CH=7k，
∴BN=2k，
∴
．
故答案为：.
练习册系列答案
相关题目
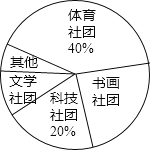
【题目】某校计划成立学生社团，要求每一位学生都选择一个社团，为了了解学生对不同社团的喜爱情况，学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查，规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项，并将统计结果绘制了如下两个不完整的统计图表．
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题：
（1）a= ，b= ；
（2）在扇形统计图中，“书画社团”所对应的扇形圆心角度数为 ；
（3）若该校共有3000名学生，试估计该校学生中选择“文学社团”的人数．
