题目内容
【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

【答案】(1)PA=5+5![]() ;(2)85°或95°或5°;
;(2)85°或95°或5°;
【解析】
(1)作BH⊥AD于H.利用特殊直角三角形边角关系 求出AH,BH,即可解决问题.
(2)分情况讨论,求出∠APA′,利用翻折不变性解决问题即可.
解:(1)如图2中,作BH⊥AD于H.
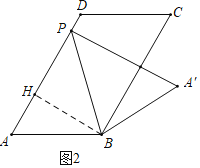
在Rt△ABH中,
∵∠AHB=90°,AB=10,∠A=60°,
∴∠ABH=30°,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵PA′⊥BC,
∴PA′⊥AD,
∴∠APA′=90°,
∴∠HPB=∠BPA′=45°,
∵BH⊥AD,
∴∠HBP=45°,
∴![]() ,
,
∴![]() ;
;
(2)①如图1-1,
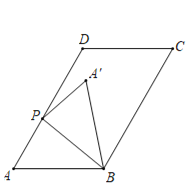
图1-1
当PA′在直线AD的右侧时,
∵∠DPA′=10°,
∴∠APA′=180°﹣∠DPA′=180°﹣10°=170°,
由翻折的性质可知:![]() ;
;
②如图1-2
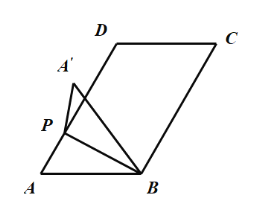
图1-2
当PA′在直线AD的左侧时,由翻折的性质可知:![]() ,
,
③如图1-3
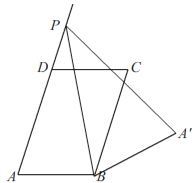
图1-3
当点P在AD的延长线上时,由折叠知,![]() ,
,
故∠APB的度数为85°或95°或5°;

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(Ⅱ)用描点法画函数图象:
(i)列表:
x | … | ﹣5 | ﹣2 | ﹣1 | 0 | … | 2 | 3 | 4 | 7 | … |
y | … | a | 2 | 3 | b | … | 6 | 3 | 2 | 1 | … |
表中a的值为 ,b的值为 .
(ii)描点连线:请在下图画出该图象的另一部分.

(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x 时,函数值y随x的增大而 ;
当x 时,函数值y随x的增大而减少.
(IV)应用:若![]() ≥6,则x的取值范围是 .
≥6,则x的取值范围是 .