题目内容
如图,在梯形ABCD中,AD∥BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.连接BF、CF、AC.(1)求证:四边形ABFC是平行四边形;
(2)若四边形ABFC是矩形,求证:△BED∽△DEC;
(3)在(2)的条件下,若等腰梯形的腰AB=5cm,下底BC=8cm,点P是BC边上的一个动点,以点P为圆心,以1cm长为半径的圆从点B出发,以每秒2cm的速度向点C移动(不与点C重合),当⊙P与AC边相切时,求⊙P移动的时间.
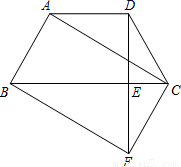
【答案】分析:(1)先根据DE⊥BC,EF=DE可知△CDF是等腰三角形,故CD=CF,∠DCB=∠FCB,再由在梯形ABCD中,AD∥BC,AB=DC可知AB=CD=CF,∠ABC=∠DCB,故∠FCB=∠ABC,所以四边形ABFC是平行四边形;
(2)连接BD,由在梯形ABCD中,AD∥BC,AB=DC可知梯形ABCD是等腰梯形,故AC=BD,由此可得出△ABC≌△DCB,再由四边形ABFC是矩形可知∠BAC=90°,故∠BDC=90°,所以∠DBC+∠DCB=90°,再由DE⊥BC可知,∠BED=90°,所以∠BDE=∠DCB,故∠DBC=∠CDE,故可得出结论;
(3)设⊙P与AC边相切于点G,⊙P移动的时间为t,则PC=BC-BP=8-2t,连接GP,则PG⊥AC,再由四边形ABFC是矩形可知AB⊥AC,故AB∥PG,所以△CGP∽△CAB,再由相似三角形的对应边成比例即可得出t的值.
解答: (1)证明:∵DE⊥BC,EF=DE,
(1)证明:∵DE⊥BC,EF=DE,
∴△CDF是等腰三角形,
∴CD=CF,∠DCB=∠FCB,
∵在梯形ABCD中,AD∥BC,AB=DC,
∴AB=CD=CF,∠ABC=∠DCB,
∴∠FCB=∠ABC,
∴四边形ABFC是平行四边形;
(2)证明:连接BD,
∵在梯形ABCD中,AD∥BC,AB=DC,
∴梯形ABCD是等腰梯形,
∴AC=BD,
在△ABC与△DCB中,
∵ ,
,
∴△ABC≌△DCB(SSS),
∵四边形ABFC是矩形,
∴∠BAC=90°,
∴∠BDC=90°,
∴∠DBC+∠DCB=90°,
∵DE⊥BC,
∴∠BED=90°,
∴∠BDE=∠DCB,∠DBC=∠CDE,
∴△BED∽△DEC;
(3)设⊙P与AC边相切于点G,⊙P移动的时间为t,则PC=BC-BP=8-2t,连接GP,则PG⊥AC,
∵四边形ABFC是矩形,
∴AB⊥AC,
∴AB∥PG,
∴△CGP∽△CAB,
∴ =
= ,
, =
= ,
,
解得t=3.2.
答:⊙P移动的时间为3.2秒.
点评:本题考查的是相似形综合题,涉及到等腰梯形的性质、相似三角形的判定与性质、切线的性质及全等三角形的判定与性质,涉及面较广,难度适中.
(2)连接BD,由在梯形ABCD中,AD∥BC,AB=DC可知梯形ABCD是等腰梯形,故AC=BD,由此可得出△ABC≌△DCB,再由四边形ABFC是矩形可知∠BAC=90°,故∠BDC=90°,所以∠DBC+∠DCB=90°,再由DE⊥BC可知,∠BED=90°,所以∠BDE=∠DCB,故∠DBC=∠CDE,故可得出结论;
(3)设⊙P与AC边相切于点G,⊙P移动的时间为t,则PC=BC-BP=8-2t,连接GP,则PG⊥AC,再由四边形ABFC是矩形可知AB⊥AC,故AB∥PG,所以△CGP∽△CAB,再由相似三角形的对应边成比例即可得出t的值.
解答:
 (1)证明:∵DE⊥BC,EF=DE,
(1)证明:∵DE⊥BC,EF=DE,∴△CDF是等腰三角形,
∴CD=CF,∠DCB=∠FCB,
∵在梯形ABCD中,AD∥BC,AB=DC,
∴AB=CD=CF,∠ABC=∠DCB,
∴∠FCB=∠ABC,
∴四边形ABFC是平行四边形;
(2)证明:连接BD,
∵在梯形ABCD中,AD∥BC,AB=DC,
∴梯形ABCD是等腰梯形,
∴AC=BD,
在△ABC与△DCB中,
∵
 ,
,∴△ABC≌△DCB(SSS),
∵四边形ABFC是矩形,
∴∠BAC=90°,
∴∠BDC=90°,
∴∠DBC+∠DCB=90°,
∵DE⊥BC,
∴∠BED=90°,
∴∠BDE=∠DCB,∠DBC=∠CDE,
∴△BED∽△DEC;
(3)设⊙P与AC边相切于点G,⊙P移动的时间为t,则PC=BC-BP=8-2t,连接GP,则PG⊥AC,
∵四边形ABFC是矩形,
∴AB⊥AC,
∴AB∥PG,
∴△CGP∽△CAB,
∴
 =
= ,
, =
= ,
,解得t=3.2.
答:⊙P移动的时间为3.2秒.
点评:本题考查的是相似形综合题,涉及到等腰梯形的性质、相似三角形的判定与性质、切线的性质及全等三角形的判定与性质,涉及面较广,难度适中.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=