Question

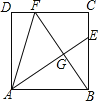
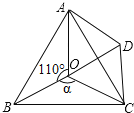
【题目】如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于点E，交BA的延长线于点F．

（1）求证：△APD≌△CPD；

（2）求证：△APE∽△FPA；

（3）若PE＝2，EF＝6，求PC的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）PC＝4

【解析】

（1）利用菱形的性质结合条件可证明△APD≌△CPD；

（2）根据全等三角形的性质得到∠DAP＝∠DCP，根据平行线的性质得到∠DCP＝∠F，等量代换得到∠DAP＝∠F，可得△APE∽△FPA；

（3）根据相似三角形的性质得到，于是得到PA2＝PEPF，等量代换即可得到PC2＝PEPF，求得PC＝4．

（1）证明：∵四边形ABCD菱形，

∴AD＝CD，∠ADP＝∠CDP，

在△APD和△CPD中，

，

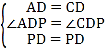∴△APD≌△CPD（SAS）；

（2）∵△APD≌△CPD，

∴∠DAP＝∠DCP，

∵CD∥BF，

∴∠DCP＝∠F，

∴∠DAP＝∠F，

又∵∠APE＝∠FPA，

∴△APE∽△FPA，

（3）∵△APE∽△FPA

∴，

∴PA2＝PEPF，

∵△APD≌△CPD，

∴PA＝PC，

∴PC2＝PEPF，

∵PE＝2，EF＝6，

∴PF＝PE+EF＝2+6＝8，

∴PC＝4．